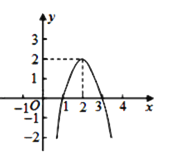题目内容
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2(k﹣1)x+k2﹣![]() k(k为常数).
k(k为常数).
(1)若抛物线在![]() 时有最低点,求k的值;(2)若抛物线经过点(1,k2),求k的值;
时有最低点,求k的值;(2)若抛物线经过点(1,k2),求k的值;
(3)若抛物线经过点(2k,y1)和点(2,y2),且y1>y2,求k的取值范围.
【答案】(1)k=4;(2)k=![]() ;(3)k>1
;(3)k>1
【解析】
(1)由抛物线解析式可得出当x=k-1时,抛物线有最低点,结合条件可求出k的值;
(2)把点坐标代入解析式即可;
(3)分别把点(2k,y1)和点(2,y2)代入函数解析式,表示y1、y2利用条件构造关于k的不等式
(1)由y=x2﹣2(k﹣1)x+k2﹣![]() k得,y=[x-(k-1)]2-
k得,y=[x-(k-1)]2-![]() k-1
k-1
∴抛物线有最低点,
即k﹣1=3,
解得,k=4;
(2)把点(1,k2)代入抛物线y=x2﹣2(k﹣1)x+k2﹣![]() k,得
k,得
k2=12﹣2(k﹣1)+k2﹣![]() k
k
解得k=![]()
(3)把点(2k,y1)代入抛物线y=x2﹣2(k﹣1)x+k2﹣![]() k,得
k,得
y1=(2k)2﹣2(k﹣1)2k+k2﹣![]() k=k2+
k=k2+![]() k
k
把点(2,y2)代入抛物线y=x2﹣2(k﹣1)x+k2﹣![]() k,得
k,得
y2=22﹣2(k﹣1)×2+k2﹣![]() k=k2﹣
k=k2﹣![]() k+8
k+8
∵y1>y2
∴k2![]() k2﹣
k2﹣![]() k+8
k+8
解得k>1.

练习册系列答案
相关题目