题目内容
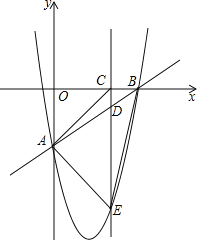
【题目】如图抛物线![]() 的开口向下与
的开口向下与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点(不与点
是抛物线上一个动点(不与点![]() 重合)
重合)

(1)求抛物线的解析式;
(2)当点![]() 是抛物线上一个动点,若
是抛物线上一个动点,若![]() 的面积为12,求点
的面积为12,求点![]() 的坐标;
的坐标;
(3)如图2,抛物线的顶点为![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() ,若存在请直接写出点
,若存在请直接写出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
【答案】(1)![]() ;(2)点P的坐标为(2,8)或(4,6)或(3
;(2)点P的坐标为(2,8)或(4,6)或(3![]() ,
,![]() 1)或(3+
1)或(3+![]() ,
,![]() 1);(3)点E坐标为(
1);(3)点E坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)将点![]() 和点
和点![]() 代入
代入![]() 求出a,b即可;
求出a,b即可;
(2)如图作辅助线,根据S△PCA=![]() PG×AC=
PG×AC=![]() ×
×![]() HP×
HP×![]() =12求出HP=4,由直线AC的表达式为y=x+6可得直线m的表达式,然后求出直线m和抛物线的交点即可得到两个P点坐标,同理可得直线n的表达式,进而得出另外两个P点坐标;
=12求出HP=4,由直线AC的表达式为y=x+6可得直线m的表达式,然后求出直线m和抛物线的交点即可得到两个P点坐标,同理可得直线n的表达式,进而得出另外两个P点坐标;
(3)首先证明∠ACD=90°,可得sin∠DAC=![]() ,然后作辅助线构造三角形,求出sin2∠DAC=
,然后作辅助线构造三角形,求出sin2∠DAC=![]() ,进而可得tan∠EAB=
,进而可得tan∠EAB=![]() ,然后分情况讨论:①当点E在AB上方时,求出直线AE的表达式即可解决问题,②当点E在AB下方时,同理计算即可.
,然后分情况讨论:①当点E在AB上方时,求出直线AE的表达式即可解决问题,②当点E在AB下方时,同理计算即可.
解:(1)将点![]() 和点
和点![]() 代入
代入![]() 得:/span>
得:/span>![]() ,
,
解得: ,
,
∴抛物线的解析式为:![]() ;
;
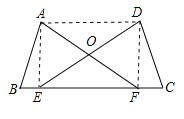
(2)如图1所示,过点P作直线m∥AC交抛物线于点P′,在直线AC下方等距离处作直线n交抛物线于点P″、P′″,过点P作PH∥y轴交AC于点H,作PG⊥AC于点G,

∵抛物线的解析式为:![]() ,
,
∴C(0,6),
∴OA=OC,
∴∠PHG=∠ACB=45°,则HP=![]() PG,
PG,
∴S△PCA=![]() PG×AC=
PG×AC=![]() ×
×![]() HP×
HP×![]() =12,
=12,
解得:HP=4,
易得直线AC的表达式为:y=x+6,
则直线m的表达式为:y=x+10,
联立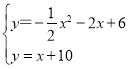 ,解得:
,解得:![]() 或
或![]() ,
,
∴点P坐标为(2,8)或(4,6);
同理可得,直线n的表达式为:y=x+2,点P(P″、P′″)的坐标为(3![]() ,
,![]() 1)或(3+
1)或(3+![]() ,
,![]() 1),
1),
综上,点P的坐标为(2,8)或(4,6)或(3![]() ,
,![]() 1)或(3+
1)或(3+![]() ,
,![]() 1);
1);
(3)∵![]() ,
,
∴D(2,8),
∵点A(6,0)、B(2,0)、C(0,6),
∴AC2=![]() ,CD2=
,CD2=![]() ,AD2=
,AD2=![]() ,
,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴sin∠DAC=![]() ,
,
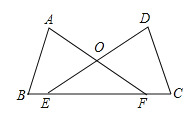
如图2,延长DC至D′使CD=CD′,连接AD′,过点D作DH⊥AD′,

则DD′=2CD=![]() ,AD=AD′=
,AD=AD′=![]() ,
,
∵S△ADD′=![]() ×DD′×AC=
×DD′×AC=![]() DH×AD′,
DH×AD′,
∴![]() ×
×![]() ×
×![]() =
=![]() DH×
DH×![]() ,
,
解得:DH=![]() ,
,
∴sin2∠DAC=sin∠DAD′=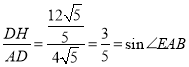 ,
,
易得tan∠EAB=![]() ,
,
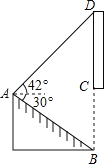
①当点E在AB上方时,如图3,
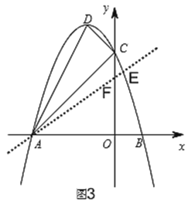
设直线AE交y轴于F,
则tan∠EAB=![]() ,
,
∴OF=![]() ,即F(0,
,即F(0,![]() ),
),
设直线AE的表达式为:y=kx+![]() ,
,
代入A(-6,0)解得:![]() ,
,
∴直线AE的表达式为:y=![]() x+
x+![]() ,
,
联立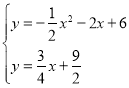 ,解得:
,解得:![]() 或
或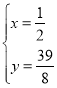 ,
,
∴点E坐标为(![]() ,
,![]() );
);
②当点E在AB下方时,
同理可得:点E(![]() ,
,![]() ),
),
综上,点E坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).