题目内容
 如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C.
如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C.(1)求直线PQ的解析式;
(2)问在线段PQ上是否存在点A使长方形ABOC的面积为
| 3 | 4 |
分析:(1)利用待定系数法即可求得直线的解析式;
(2)设A的横坐标是t,则根据直线PQ的解析式即可求得纵坐标,根据长方形ABOC的面积为
,即可列方程求得t的值,从而求得A的坐标.
(2)设A的横坐标是t,则根据直线PQ的解析式即可求得纵坐标,根据长方形ABOC的面积为
| 3 |
| 4 |
解答:解:(1)设直线PQ的解析式是y=kx+b,
则
,
解得:
,
则直线PQ的解析式是y=-x+2;
(2)设A的横坐标是t,则纵坐标是-t+2=2-t.
根据题意得:t(2-t)=
,
解得:t=
或
.
当t=
时,2-t=
;
当t=
时,2-t=
.
故A的坐标是(
,
)或(
,
).
则
|
解得:
|
则直线PQ的解析式是y=-x+2;
(2)设A的横坐标是t,则纵坐标是-t+2=2-t.
根据题意得:t(2-t)=
| 3 |
| 4 |
解得:t=
| 3 |
| 2 |
| 1 |
| 2 |
当t=
| 3 |
| 2 |
| 1 |
| 2 |
当t=
| 1 |
| 2 |
| 3 |
| 2 |
故A的坐标是(
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查了待定系数法求函数的解析式以及列方程解应用题,体现了方程思想的应用.

练习册系列答案
相关题目
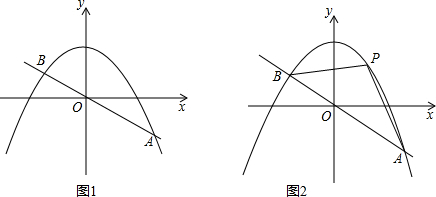
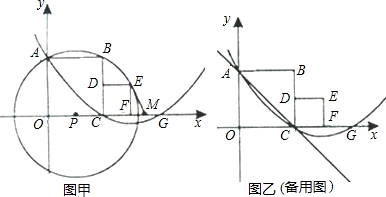
 【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段)
【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段) 如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C.
如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C. ?若存在,请直接写出点A的坐标;若不存在,说明理由.
?若存在,请直接写出点A的坐标;若不存在,说明理由.