题目内容
如图1,已知直线y=-| 1 |
| 2 |
| 1 |
| 4 |
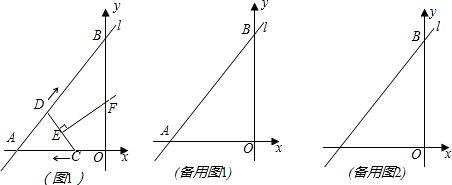
(1)求A,B两点的坐标;
(2)求线段AB的垂直平分线的解析式;
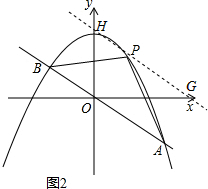
(3)如图2,取与线段AB等长的一根橡皮筋,端点分别固定在A,B两处.用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A,B构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.
分析:(1)联立两函数的解析式即可求出A、B点的坐标.
(2)可作AB的垂直平分线设其与x轴,y轴的交点分别为C、D,与AB的交点为M,可根据△BEO∽△OCM求出OC的长,同理可求出OD的长,即可得出C、D的坐标,用待定系数法即可求出AB垂直平分线的解析式.(另一种解法,可根据A、B的坐标得出AB中点的坐标,先求出直线AB的解析式,由于AB的垂直平分线与AB垂直,因此它的斜率与AB的斜率的乘积为-1,由此可得出所求直线的斜率,然后将中点坐标代入即可求出其解析式.)
(3)要使三角形ABP的面积最大,那么P到AB的距离就最大,因此P点必在与直线AB平行且与抛物线只有一个交点的一次函数上(设此直线与x轴,y轴的交点为G、H),据此可求出此直线的解析式和P点的坐标.然后可通过在三角形OHG中,根据面积的不同表示方法求出P点到AB的距离(即O到GH的距离),进而可求出三角形ABP的面积.
(2)可作AB的垂直平分线设其与x轴,y轴的交点分别为C、D,与AB的交点为M,可根据△BEO∽△OCM求出OC的长,同理可求出OD的长,即可得出C、D的坐标,用待定系数法即可求出AB垂直平分线的解析式.(另一种解法,可根据A、B的坐标得出AB中点的坐标,先求出直线AB的解析式,由于AB的垂直平分线与AB垂直,因此它的斜率与AB的斜率的乘积为-1,由此可得出所求直线的斜率,然后将中点坐标代入即可求出其解析式.)
(3)要使三角形ABP的面积最大,那么P到AB的距离就最大,因此P点必在与直线AB平行且与抛物线只有一个交点的一次函数上(设此直线与x轴,y轴的交点为G、H),据此可求出此直线的解析式和P点的坐标.然后可通过在三角形OHG中,根据面积的不同表示方法求出P点到AB的距离(即O到GH的距离),进而可求出三角形ABP的面积.
解答:解:(1)依题意得
解之得
∴A(6,-3),B(-4,2)
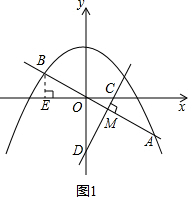
(2)作AB的垂直平分线交x轴,y轴于C,D两点,交AB于M(如图1),
由(1)可知:OA=3
,OB=2
∴AB=5
AB-OB=
过B作BE⊥x轴,E为垂足
由“△BEO∽△CMO,得:
=
,
∴OC=
同理:OD=
,
∴C(
,0),D(0,-
)
设CD的解析式为y=kx+b(k≠0)
∴
∴
∴AB的垂直平分线的解析式为:y=2x-
.
(3)若存在点P使△APB的面积最大,则点P在与直线AB平行且和抛物线只有一个交点的直线
y=-
x+m上,并设该直线与x轴,y轴交于G,H两点(如图2).
∴
 ∴
∴
x2-
x+m-6=0
∵抛物线与直线只有一个交点,
∴△=(-
)2-4×
(m-6)=0,
∴m=
,
故
x2-
x+
=0,即(x-1)2=0,
解得:x=1,
将x=1代入y=-
+
得:y=
,
∴P(1,
)
在直线GH:y=-
x+
中,
∴G(
,0),H(0,
)
∴GH=
设O到GH的距离为d,
∵
GH•d=
OG•OH
∵
×
d=
×
×
∴d=
,
又∵由AB∥GH
∴P到AB的距离等于O到GH的距离d.
∴S最大面积=
AB•d=
×5
×
=
.
|
解之得
|
|
∴A(6,-3),B(-4,2)
(2)作AB的垂直平分线交x轴,y轴于C,D两点,交AB于M(如图1),
由(1)可知:OA=3
| 5 |
| 5 |
∴AB=5
| 5 |

| 1 |
| 2 |
| ||
| 2 |
过B作BE⊥x轴,E为垂足
由“△BEO∽△CMO,得:
| OC |
| OB |
| OM |
| OE |
∴OC=
| 5 |
| 4 |
同理:OD=
| 5 |
| 2 |
∴C(
| 5 |
| 4 |
| 5 |
| 2 |
设CD的解析式为y=kx+b(k≠0)
∴
|
∴
|
∴AB的垂直平分线的解析式为:y=2x-
| 5 |
| 2 |
(3)若存在点P使△APB的面积最大,则点P在与直线AB平行且和抛物线只有一个交点的直线
y=-
| 1 |
| 2 |
∴
|
 ∴
∴| 1 |
| 4 |
| 1 |
| 2 |
∵抛物线与直线只有一个交点,
∴△=(-
| 1 |
| 2 |
| 1 |
| 4 |
∴m=
| 25 |
| 4 |
故
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解得:x=1,
将x=1代入y=-
| 1 |
| 2 |
| 25 |
| 4 |
| 23 |
| 4 |
∴P(1,
| 23 |
| 4 |
在直线GH:y=-
| 1 |
| 2 |
| 25 |
| 4 |
∴G(
| 25 |
| 2 |
| 25 |
| 4 |
∴GH=
| 25 |
| 4 |
| 5 |
设O到GH的距离为d,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∵
| 1 |
| 2 |
25
| ||
| 4 |
| 1 |
| 2 |
| 25 |
| 2 |
| 25 |
| 4 |
∴d=
5
| ||
| 2 |
又∵由AB∥GH
∴P到AB的距离等于O到GH的距离d.
∴S最大面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
5
| ||
| 2 |
| 125 |
| 4 |
点评:本题主要考查二次函数、一元二次方程的根判别式及一些几何知识,是全卷的压轴题,综合性很强,要求学生全面而扎实地掌握所学知识,第(3)小题很有创意又有一定的探索性,总之,这是一道能很好地考查学生初中三年积累的好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图1,已知直线:
如图1,已知直线: