题目内容
【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
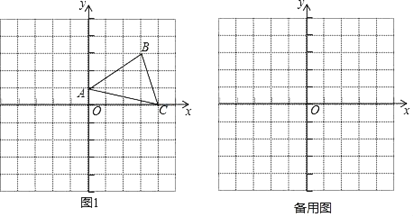
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
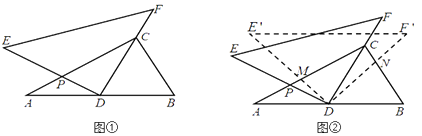
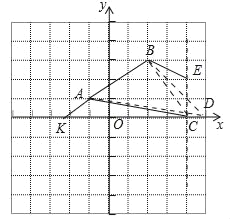
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
【答案】(1)2;(2)﹣10≤m<1;(3)(![]() +4,0)或(﹣
+4,0)或(﹣![]() ﹣9,0)
﹣9,0)
【解析】
(1)求出OA、OC即可解决问题;
(2)求出△ABC的面积,根据不等式即可解决问题;
(3)如图2中,延长BA交x轴于K,连接BC.首先求出直线AB的解析式,可得点K坐标,根据S△ABD=S四边形ABEC,可得S△BKD﹣S△AKD=S△BCK+S△BCE﹣S△ACK,由此构建方程即可解决问题;
解:(1)∵A(0,1),C(4,0),
∴OA=1,OC=4,
∴![]()
故答案为2.
(2)如图1,作BH⊥y轴于H.
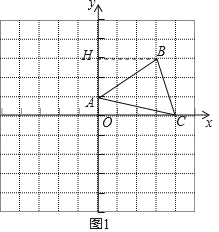
S△ABC=S四边形OCBH﹣S△ABH﹣S△OAC
![]()
![]()
由题意, ![]()
∴m≥﹣10,
∵P在第二象限,
∴m﹣1<0,
∴m<1,
∴﹣10≤m<1.
(3)如图2中,延长BA交x轴于K,连接BC.
∵A(﹣1,1),B(2,3),
设直线AB的解析式为y=kx+b,则有![]()
解得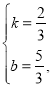
∴直线AB的解析式为![]()
∴![]() 当点D在K的右边,设D(m,0),
当点D在K的右边,设D(m,0),
∵S△ABD=S四边形ABEC,
∴S△BKD﹣S△AKD=S△BCK+S△BCE﹣S△ACK,
∴![]()
解得![]()
∴![]()
根据对称性可知,当点D′在K的左侧时,D′K=DK,可得![]()
综上所述,满足条件的D的坐标![]() 或
或![]()
方法二:当点D在K的右边,设D(m,0),(m>4),
∵![]()
S四边形ABEC=S△ABC+S△BCE![]()
![]() 解得
解得![]() 接下来同上面.
接下来同上面.
故答案为:![]() 或
或![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案