题目内容
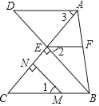
【题目】如图,![]() 中,
中,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿折线
个单位长度的速度沿折线![]() 运动(回到点
运动(回到点![]() 停止运动),设运动时间为
停止运动),设运动时间为![]() 秒.
秒.
(1)当点![]() 在
在![]() 上时,且满足
上时,且满足![]() 时,求出此时
时,求出此时![]() 的值;
的值;
(2)当点![]() 在
在![]() 上时,求出
上时,求出![]() 为何值时,
为何值时,![]() 为以
为以![]() 为腰的等腰三角形.
为腰的等腰三角形.

【答案】(1)![]() ;(2)
;(2)![]() 秒或
秒或![]() 秒
秒
【解析】
(1)根据勾股定理可得,AC=3,根据题意可知,PA=PB=AC+CB-t=7-t,PC=t-3,根据勾股定理列关于t的方程,解方程即可得到t的值;
(2)若点P在AB上,根据运动的路程易得t的值,当AP=AC=3时,△ACP为等腰三角形,根据等量关系列出关于t的方程即可求出t的值;当CP=AC时,过点![]() 作
作![]() 于点
于点![]() 根据直角三角形面积公式可得CD的长,由勾股定理可得AD的长,根据等腰三角形的性质可得AP的长,根据等量关系列出关于t的方程即可求出t的值.
根据直角三角形面积公式可得CD的长,由勾股定理可得AD的长,根据等腰三角形的性质可得AP的长,根据等量关系列出关于t的方程即可求出t的值.
解:![]() 在
在![]() 中,
中,![]()
![]() 由勾股定理,得
由勾股定理,得![]()
如图1,连接![]()
当![]() 时,
时,![]()
在![]() 中,
中,![]()
即![]()
解得![]()
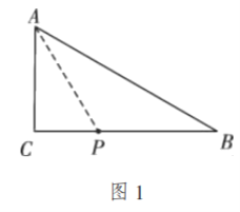
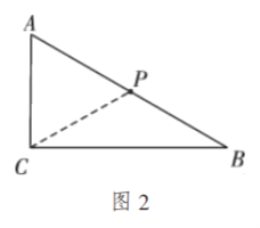
![]() ①如图2,当
①如图2,当![]() 时,
时,![]() 为等腰三角形,
为等腰三角形,
![]()
![]()
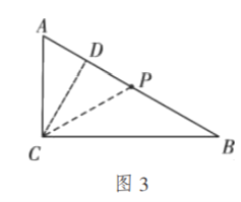
②如图3,当点![]() 在
在![]() 上,
上,![]() 时,
时,
过点![]() 作
作![]() 于点
于点![]()
![]()
![]()
![]()
在![]() 中
中
由勾股定理,得
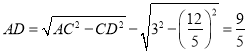
![]()
![]()
![]()
综上所述,当点![]() 在
在![]() 上,
上,![]() 为
为![]() 秒或
秒或![]() 秒时,
秒时,![]() 为以
为以![]() 为腰的等腰三角形
为腰的等腰三角形

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目