题目内容
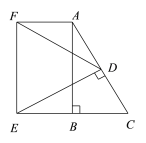
【题目】Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,从D作DE⊥AC与CB的延长线交于点E,以AB、BE为邻边作矩形ABEF,连结DF,则DF的长是( )
A. 4![]() B. 3
B. 3![]() C. 2
C. 2![]() D. 4
D. 4
【答案】C
【解析】
由已知条件易证BC=![]() AC=CD,这样结合∠EDC=∠ABC=90°,∠C=∠C,即可证得△EDC≌△ABC,结合四边形ABEF是矩形可得DE=AB=EF,再证∠DEF=60°即可得到△DEF是等边三角形,从而可得DF=DE,这样在Rt△DEC中由DC=BC=2结合∠C=60°求出DE的长即可得到DF的长.
AC=CD,这样结合∠EDC=∠ABC=90°,∠C=∠C,即可证得△EDC≌△ABC,结合四边形ABEF是矩形可得DE=AB=EF,再证∠DEF=60°即可得到△DEF是等边三角形,从而可得DF=DE,这样在Rt△DEC中由DC=BC=2结合∠C=60°求出DE的长即可得到DF的长.
∵在△ABC中,∠ABC=90°,∠C=60°,
∴∠BAC=30°,
∴BC=![]() AC,
AC,
又∵点D是AC的中点,
∴BC=DC,
∵DE⊥AC,
∴∠EDC=90°=∠ABC,
又∵∠C=∠C,
∴△EDC≌△ABC,
∴DE=AB,∠DEC=∠BAC=30°,
∵四边形ABEF是矩形,
∴DE=AB=EF,∠FEC=90°,
∴∠FED=90°-30°=60°,
∴△DEF是等边三角形,
∴DF=DE,
∵在Rt△DEC中,∠DEC=30°,∠EDC=90°,CD=2,
∴CE=4,
∴DE=![]() ,
,
∴DF=![]() .
.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目