题目内容
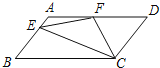
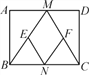
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)当AB∶AD=___时,四边形MENF是正方形,并说明理由.
【答案】(1)证明见解析;(2)见解析
【解析】试题分析:(1)利用矩形的性质,利用HL证明△ABM≌△DCM.(2)利用四边形MENF是正方形的结论反推出条件AB∶AD=1∶2,再用条件证明,先证明∠AMB=45°.利用△ABM≌△DCM,证明四边形MENF是菱形,最后得菱形MENF是正方形.
试题解析:
解:(1)证明:∵四边形ABCD是矩形,∴AB=DC,∠A=∠D=90°.∵M为AD的中点,∴AM=MD,∴△ABM≌△DCM.
(2) 1∶2,理由:∵AB∶AD=1∶2,∴AB=![]() AD.∵AM=
AD.∵AM=![]() AD,∴AB=AM,∴∠ABM=∠AMB.∵∠A=90°,∴∠AMB=45°.∵△ABM≌△DCM,∴BM=CM,∠DMC=∠AMB=45°,∴∠BMC=90°.∵E,F,N分别是BM,CM,BC的中点,∴EN∥CM,FN∥BM,EM=MF,
AD,∴AB=AM,∴∠ABM=∠AMB.∵∠A=90°,∴∠AMB=45°.∵△ABM≌△DCM,∴BM=CM,∠DMC=∠AMB=45°,∴∠BMC=90°.∵E,F,N分别是BM,CM,BC的中点,∴EN∥CM,FN∥BM,EM=MF,
∴四边形MENF是菱形.
∵∠BMC=90°,
∴菱形MENF是正方形.

练习册系列答案
相关题目