题目内容
(本小题满分9分)
如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求经过A、O、B三点的抛物线的解析式;
(2)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(3)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
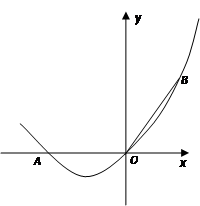
解:(1)B(1,![]() )………………………………………………….1分
)………………………………………………….1分
设抛物线的解析式为y=ax(x+a),代入点B(1, 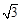 ),得
),得![]() ,
,
因此![]() …………………………………………………3分
…………………………………………………3分
(2)如图,抛物线的对称轴是直线x=—1,当点C位于对称轴与线段AB的交点时,△BOC的周长最小…………………………………………………4分
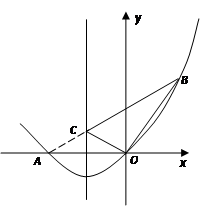
设直线AB为y=kx+b.所以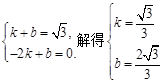 ,
,
因此直线AB为![]() ,………………5分
,………………5分
当x=-1时,![]() ,
,
因此点C的坐标为(-1,![]() ). …………………6分
). …………………6分
(3)如图,过P作y轴的平行线交AB于D.
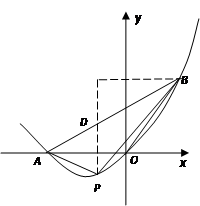
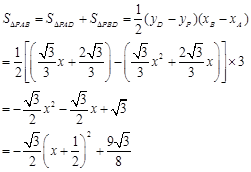 …………………7分
…………………7分
当x=-![]() 时,△PAB的面积的最大值为
时,△PAB的面积的最大值为![]() ……..9分
……..9分
解析:略

练习册系列答案
相关题目




 不小于3cm吗?请说明理由.
不小于3cm吗?请说明理由. 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的 ,另一根露出水面的长度是它的
,另一根露出水面的长度是它的 .两根铁棒长度之和为55 cm.
.两根铁棒长度之和为55 cm.
 甲:
甲: 乙:
乙: =55
=55