题目内容
(本小题满分14分)
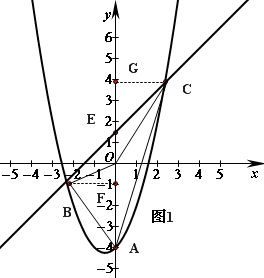
如图1,抛物线![]() 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线![]() 与抛物线交于点B、C.
与抛物线交于点B、C.

1.(1)求点A的坐标;
2.(2)当b=0时(如图2),求![]() 与
与![]() 的面积。
的面积。
3.(3)当![]() 时,
时,![]() 与
与![]() 的面积大小关系如何?为什么?
的面积大小关系如何?为什么?
4.(4)是否存在这样的b,使得![]() 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
1.(1)将x=0,代入抛物线解析式,得点A的坐标为(0,-4)
2.(2)当b=0时,直线为![]() ,
,
由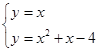 解得
解得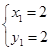 ,
,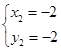 ..............................2分
..............................2分
所以B、C的坐标分别为B(-2,-2),C(2,2)..........................2分
![]() ,
,![]() .
.
3.(3)当![]() 时,
时,![]() ........................................4分
........................................4分
由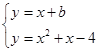 ,解得
,解得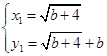 ,
,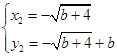 ............6分
............6分
所以B、C的坐标分别为:
B(-![]() ,-
,-![]() +b),C(
+b),C(![]() ,
,![]() +b),...................6分
+b),...................6分
作![]() 轴,
轴,![]() 轴,垂足分别为F、G,
轴,垂足分别为F、G,
则![]() ,................................................7分
,................................................7分
而![]() 和
和![]() 是同底的两个三角形,
是同底的两个三角形,
所以![]() ..............
..............
4.存在这样的b. ..................................................9分
因为![]()
所以![]() .................................................10分
.................................................10分
所以![]() ,即E为BC的中点....................................10分
,即E为BC的中点....................................10分
所以当OE=CE时,![]() 为直角三角形...............................11分
为直角三角形...............................11分
因为![]() ...............................12分
...............................12分
所以 ![]() ,而
,而![]() ..................................13分
..................................13分
所以![]() ,解得
,解得![]() ,..........................14分
,..........................14分
所以当b=4或-2时,ΔOBC为直角三角形. ..........................14分
解析:略

 如图13,二次函数
如图13,二次函数 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为( ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线 与抛物线交于点B、C.
与抛物线交于点B、C.
 与
与 的面积。
的面积。 时,
时, 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.