Question

【题目】（问题原型）如图1，在四边形ABCD中，，点E、F分别为AC、BC的中点，连结EF，试说明：．

（探究）如图2，在问题原型的条件下，当AC平分，时，求的大小．

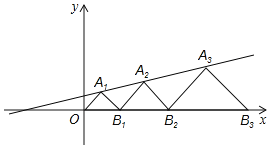
（应用）如图3，在问题原型的条件下，当，且四边形CDEF是菱形时，直接写出四边形ABCD的面积．

Answer 1

【答案】【问题原型】证明见解析；【探究】；【应用】．

【解析】

问题原型:利用直角三角形斜边的中线性质和三角形的中位线性质可得结论；

探究:先证明∠CEF=∠BAD，∠DEC=∠BAD，根据∠DEF=〖90〗^列方程得∠BAD的度数；

应用:由四边形CDEF是菱形，说明△CDE是等边三角形，再根据等底同高说明△CDE与△DEA间关系，根据相似说明△CAB与△CEF间关系，由AB=2，得DE=1，得等边△DE的面积，利用三角形的面积间关系得结论．

问题原型:证明：

在中，点E，F分别为AC，BC的中点

，且

在中，点E为AC的中点，

探究:平分，，

，

，

应用:四边形ABCD的面积为：

四边形CDEF是菱形，，

与都是等边三角形，

，

，

，，

．