题目内容
【题目】周末,小芳骑自行车从家出发到野外郊游,从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地,小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地,如图是她们距乙地的路程y(km)与小芳离家时间x(h)的函数图象. 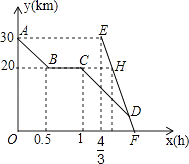
(1)小芳骑车的速度为km/h,H点坐标 .
(2)小芳从家出发多少小时后被妈妈追上?此时距家的路程多远?
(3)相遇后,妈妈载上小芳和自行车同时到达乙地(彼此交流时间忽略不计),求小芳比预计时间早几分钟到达乙地?
【答案】
(1)20;( ![]() ,20)
,20)
(2)解:设直线AB的解析式为:y1=k1x+b1,
将点A(0,30),B(0.5,20)代入得:y1=﹣20x+30,
∵AB∥CD,
∴设直线CD的解析式为:y2=﹣20x+b2,
将点C(1,20)代入得:b2=40,
故y2=﹣20x+40,
设直线EF的解析式为:y3=k3x+b3,
将点E( ![]() ,30),H(
,30),H( ![]() ,20)代入得:k3=﹣60,b3=110,
,20)代入得:k3=﹣60,b3=110,
∴y3=﹣60x+110,
解方程组 ![]() ,得
,得 ![]() ,
,
∴点D坐标为(1.75,5),
30﹣5=25(km),
所以小芳出发1.75小时后被妈妈追上,此时距家25km
(3)解:将y=0代入直线CD解析式有:﹣20x+40=0,
解得x=2,
将y=0代入直线EF的解析式有:﹣60x+110=0,
解得x= ![]() ,
,
2﹣ ![]() =
= ![]() (h)=10(分钟),
(h)=10(分钟),
故小芳比预计时间早10分钟到达乙地
【解析】解:(1)由函数图可以得出,小芳家距离甲地的路程为10km,花费时间为0.5h, 故小芳骑车的速度为:10÷0.5=20(km/h),
由题意可得出,点H的纵坐标为20,横坐标为: ![]() +
+ ![]() =
= ![]() ,
,
故点H的坐标为( ![]() ,20);
,20);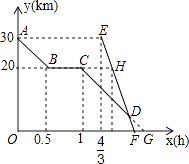

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目