题目内容
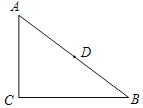
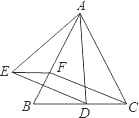
【题目】将图1,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
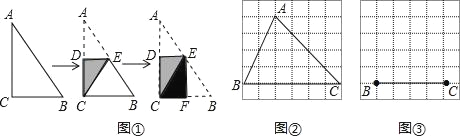
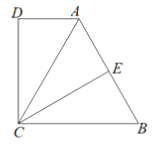
(1)如图2,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕;
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)如果一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是 ;
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是 .
【答案】见解析
【解析】(1)图2中将三角形的三个角分别向三角形内部进行折叠即可;
(2)图3中只要使三角形一边上的高等于该边长即可;
(3)利用折叠后的两个重合的正方形可知,三角形一边长的一半和这一边上的高的一半都等于正方形的边长,所以三角形的一边和这边上的高应该相等;
(4)如果一个四边形能折叠成叠加矩形,可以将四边形的四个角分别向四边形内部折叠即可得到该结果,折痕应经过四边中点,而连接四边形各边中点得到矩形的话,该四边形的对角线应互相垂直.
(1)(2)

(3)三角形的一边长与该边上的高相等的直角三角形或锐角三角形;
(4)对角线互相垂直.(注:回答菱形、正方形不给分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目