题目内容
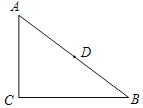
【题目】如图Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB的中点,P是直线BC上一点,把△BDP沿PD所在直线翻折后,点B落在点Q处,如果QD⊥BC,那么点P和点B间的距离等于____.
【答案】2.5或10
【解析】
在Rt△ACB中,根据勾股定理可求AB的长,根据折叠的性质可得QD=BD,QP=BP,根据三角形中位线定理可得DE=![]() AC,BD=
AC,BD=![]() AB,BE=
AB,BE=![]() BC,再在Rt△QEP中,根据勾股定理可求QP,继而可求得答案.
BC,再在Rt△QEP中,根据勾股定理可求QP,继而可求得答案.
如图所示:
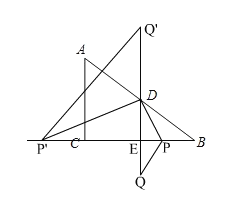
在Rt△ACB中,∠C=90°,AC=6,BC=8,
AB=![]() =10,
=10,
由折叠的性质可得QD=BD,QP=BP,
又∵QD⊥BC,
∴DQ∥AC,
∵D是AB的中点,
∴DE=![]() AC=3,BD=
AC=3,BD=![]() AB=5,BE=
AB=5,BE=![]() BC=4,
BC=4,
①当点P在DE右侧时,
∴QE=5-3=2,
在Rt△QEP中,QP2=(4-BP)2+QE2,
即QP2=(4-QP)2+22,
解得QP=2.5,
则BP=2.5.
②当点P在DE左侧时,同①知,BP=10
故答案为:2.5或10.

练习册系列答案
相关题目