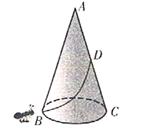
题目内容
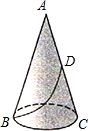 已知用圆心角为120°,面积为3π的扇形卷成一个无底圆锥形筒.
已知用圆心角为120°,面积为3π的扇形卷成一个无底圆锥形筒.
(1)求这个圆锥形筒的高;
(2)一只蚂蚁要从圆锥底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC的中点D,问蚂蚁沿怎样的路线爬行,使路程最短?最短路程是多少?
解:(1)∵3π=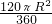 ,
,
∴R=3,
即母线l=3
∵3π= lR,
lR,
∴l=2π,
∴2πr=2π,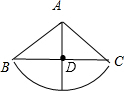
∴底面半径r=1,
高h=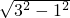 =2
=2 ;
;
(2)由题意可知:∠DAC=120°÷2=60°,
根据勾股定理求得:AD= ,CD=
,CD= ,
,
所以蚂蚁爬行的最短距离为BD=CD= .
.
分析:(1)利用扇形的面积公式可求出扇形的半径,进而求出扇形所在弧的长度圆锥的底面周长,所以底面圆的半径可求,再利用勾股定理即可求出这个圆锥形筒的高;
(2)利用弧长公式即可求得侧面展开图的圆心角,再利用等腰三角形的性质求得相应线段即可.
点评:此题主要考查了圆锥侧面展开图以及最短路径求法,求立体图形中两点之间的最短路线长,一般应放在平面内,利用直角三角形求两点之间的线段的长度.用到的知识点为:圆锥的弧长等于底面周长.
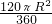 ,
,∴R=3,
即母线l=3
∵3π=
 lR,
lR,∴l=2π,
∴2πr=2π,

∴底面半径r=1,
高h=
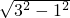 =2
=2 ;
;(2)由题意可知:∠DAC=120°÷2=60°,
根据勾股定理求得:AD=
 ,CD=
,CD= ,
,所以蚂蚁爬行的最短距离为BD=CD=
 .
.分析:(1)利用扇形的面积公式可求出扇形的半径,进而求出扇形所在弧的长度圆锥的底面周长,所以底面圆的半径可求,再利用勾股定理即可求出这个圆锥形筒的高;
(2)利用弧长公式即可求得侧面展开图的圆心角,再利用等腰三角形的性质求得相应线段即可.
点评:此题主要考查了圆锥侧面展开图以及最短路径求法,求立体图形中两点之间的最短路线长,一般应放在平面内,利用直角三角形求两点之间的线段的长度.用到的知识点为:圆锥的弧长等于底面周长.

练习册系列答案
相关题目
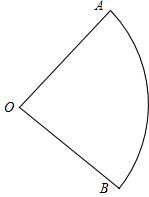 如图已知扇形OAB
如图已知扇形OAB
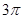 的扇形卷成一个无底圆锥形筒.
的扇形卷成一个无底圆锥形筒.