题目内容
选做题:从 甲、乙两题中选做一题,如果两题都做,只以甲题计分。
甲、乙两题中选做一题,如果两题都做,只以甲题计分。
题甲:已知关于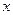 的方程
的方程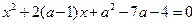 的两根为
的两根为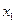 、
、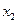 ,且满足
,且满足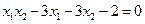 .求
.求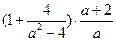 的值。
的值。
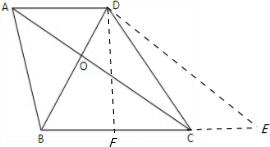
题乙:如图12,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.
(1)求证:AC⊥BD
(2)求△AOB的面积
我选做的是 题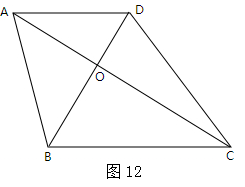
 甲、乙两题中选做一题,如果两题都做,只以甲题计分。
甲、乙两题中选做一题,如果两题都做,只以甲题计分。题甲:已知关于
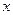 的方程
的方程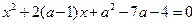 的两根为
的两根为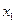 、
、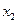 ,且满足
,且满足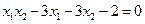 .求
.求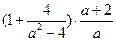 的值。
的值。题乙:如图12,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.
(1)求证:AC⊥BD
(2)求△AOB的面积
我选做的是 题

题甲:已知关于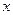 的方程
的方程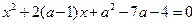 的两根为
的两根为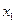 、
、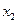 ,且满足
,且满足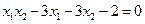 .求
.求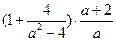 的值。
的值。
解:题甲:关于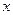 的方程
的方程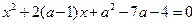 的两根为
的两根为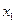 、
、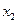 ,
,
∴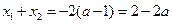 ,
,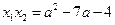
∴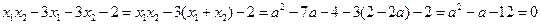
解得: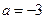 (舍去)或
(舍去)或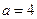 ,
,
又∵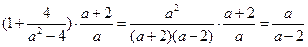
当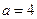 时,原式=
时,原式=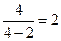 .
.
题乙:(1)过点D作DE∥AC,交BC的延长线于E,
∵AD∥BC,
∴四边形ACED是平行四边形,
∴DE=BD,DE∥BD,CE=AD,
∵AD=2,BC=BD=3,AC=4,
∴BE=BC+CE=5,DE=AC=4,BD=3,
∴BD2+DE2=BE2,
∴∠BDC=90°,
∴BD⊥DE,
∴BD⊥AC;
(2)过点D作DF⊥BC于F,
∵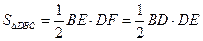 ,
,
∴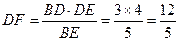
∴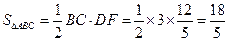
∵AD∥BC,
∴△AOD∽△COB,
∴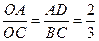 ,
,
∴OA:AC=2:5,
∴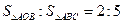
∴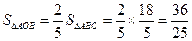
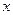 的方程
的方程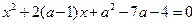 的两根为
的两根为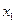 、
、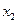 ,且满足
,且满足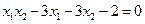 .求
.求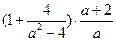 的值。
的值。
解:题甲:关于
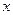 的方程
的方程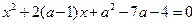 的两根为
的两根为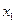 、
、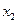 ,
,∴
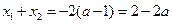 ,
,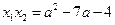
∴
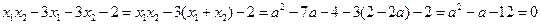
解得:
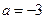 (舍去)或
(舍去)或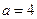 ,
,又∵
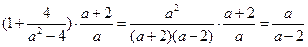
当
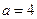 时,原式=
时,原式=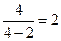 .
.题乙:(1)过点D作DE∥AC,交BC的延长线于E,
∵AD∥BC,
∴四边形ACED是平行四边形,
∴DE=BD,DE∥BD,CE=AD,
∵AD=2,BC=BD=3,AC=4,
∴BE=BC+CE=5,DE=AC=4,BD=3,
∴BD2+DE2=BE2,
∴∠BDC=90°,
∴BD⊥DE,
∴BD⊥AC;
(2)过点D作DF⊥BC于F,
∵
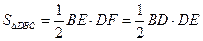 ,
,∴
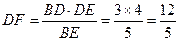
∴
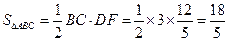
∵AD∥BC,
∴△AOD∽△COB,
∴
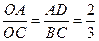 ,
,∴OA:AC=2:5,
∴
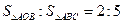
∴
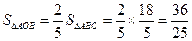
略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
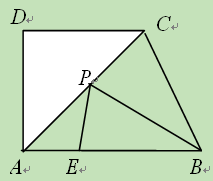
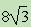 ,求AC的长.
,求AC的长.






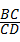 ;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )
;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )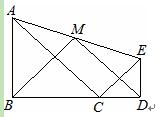


 .
.
 ?若存在,请求出该点坐标,若不存在,请说明理由.
?若存在,请求出该点坐标,若不存在,请说明理由.