题目内容
【题目】如图,在等腰△ABC中,AB=AC,如果2AB=3BC,求∠B的三个三角函数值.
【答案】sin B=![]() =
=![]() =
=![]() ,cos B=
,cos B=![]() =
=![]() =
=![]() ,
,
tan B=![]() =
=![]() =2
=2![]() .
.
【解析】试题分析:
三角形函数的定义是建立在直角三角形基础上的,因此我们需要构造一个包含∠B的直角三角形,结合已知条件和等腰三角形的性质,我们选择作出BC边上的高,利用已知条件和“等腰三角形中的三线合一”,可以把AB、AD、BD用含同一待定字母的式子表达出来,就可由“锐角三角函数的定义”求出∠B的三个三角函数值了.
试题解析:
过点A作AD⊥BC于点D,如图所示.
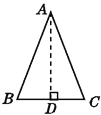
∵AB=AC,
∴BD=CD.
又∵2AB=3BC,
∴![]() =
=![]() .
.
设AB=AC=3k,则BC=2k.
∴BD=CD=k,
∴AD=![]() =
=![]() =
=![]() =2
=2![]() k.
k.
∴sin B=![]() =
=![]() =
=![]() ,cos B=
,cos B=![]() =
=![]() =
=![]() ,tan B=
,tan B=![]() =
=![]() =2
=2![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


