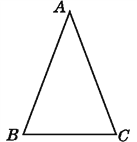题目内容
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
【答案】(1)![]() ;(2)证明见试题解析.
;(2)证明见试题解析.
【解析】
试题分析:(1)由角平分线的性质可知CD=DE=4cm,由于∠C=90°,故∠B=∠BDE=45°,△BDE是等腰直角三角形,由勾股定理得可得BD,AC的值;
(2)由(1)可知:△ACD≌△AED,AC=AE,BE=DE=CD,故AB=AE+BE=AC+CD.
试题解析:(1)∵AD是△ABC的角平分线,DC⊥AC,DE⊥AB,∴DE=CD=4cm,又∵AC=BC,∴∠B=∠BAC,又∵∠C=90°,∴∠B=∠BDE=45°,∴BE=DE=4cm.
在等腰直角三角形BDE中,由勾股定理得,BD=![]() cm,∴AC=BC=CD+BD=
cm,∴AC=BC=CD+BD=![]() (cm).
(cm).
(2)∵AD是△ABC的角平分线,DC⊥AC,DE⊥AB,∴∠ADE=∠ADC,∴AC=AE,又∵BE=DE=CD,∴AB=AE+BE=AC+CD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目