题目内容
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ![]() ),B(4,0)两点.
),B(4,0)两点.
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 ![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
【答案】
(1)
解:∵A(1,3 ![]() ),B(4,0)在抛物线y=mx2+nx的图象上,
),B(4,0)在抛物线y=mx2+nx的图象上,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣ ![]() x2+4
x2+4 ![]() x;
x;
(2)
解:存在三个点满足题意,理由如下:
当点D在x轴上时,如图1,过点A作AD⊥x轴于点D,
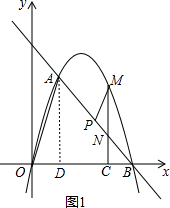
∵A(1,3 ![]() ),
),
∴D坐标为(1,0);
当点D在y轴上时,设D(0,d),则AD2=1+(3 ![]() ﹣d)2,BD2=42+d2,且AB2=(4﹣1)2+(3
﹣d)2,BD2=42+d2,且AB2=(4﹣1)2+(3 ![]() )2=36,
)2=36,
∵△ABD是以AB为斜边的直角三角形,
∴AD2+BD2=AB2,即1+(3 ![]() ﹣d)2+42+d2=36,解得d=
﹣d)2+42+d2=36,解得d= ![]() ,
,
∴D点坐标为(0, ![]() )或(0,
)或(0, ![]() );
);
综上可知存在满足条件的D点,其坐标为(1,0)或(0, ![]() )或(0,
)或(0, ![]() );
);
(补充方法:可用A,B点为直径作一个圆,圆与坐标轴的交点即为答案)
(3)
解:如图2,过P作PF⊥CM于点F,
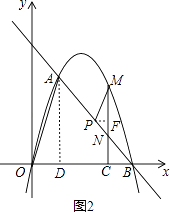
∵PM∥OA,
∴Rt△ADO∽Rt△MFP,
∴ ![]() =
= ![]() =3
=3 ![]() ,
,
∴MF=3 ![]() PF,
PF,
在Rt△ABD中,BD=3,AD=3 ![]() ,
,
∴tan∠ABD= ![]() ,
,
∴∠ABD=60°,设BC=a,则CN= ![]() a,
a,
在Rt△PFN中,∠PNF=∠BNC=30°,
∴tan∠PNF= ![]() =
= ![]() ,
,
∴FN= ![]() PF,
PF,
∴MN=MF+FN=4 ![]() PF,
PF,
∵S△BCN=2S△PMN,
∴ ![]() a2=2×
a2=2× ![]() ×4
×4 ![]() PF2,
PF2,
∴a=2 ![]() PF,
PF,
∴NC= ![]() a=2
a=2 ![]() PF,
PF,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴MN= ![]() NC=
NC= ![]() ×
× ![]() a=
a= ![]() a,
a,
∴MC=MN+NC=( ![]() +
+ ![]() )a,
)a,
∴M点坐标为(4﹣a,( ![]() +
+ ![]() )a),
)a),
又M点在抛物线上,代入可得﹣ ![]() (4﹣a)2+4
(4﹣a)2+4 ![]() (4﹣a)=(
(4﹣a)=( ![]() +
+ ![]() )a,
)a,
解得a=3﹣ ![]() 或a=0(舍去),
或a=0(舍去),
OC=4﹣a= ![]() +1,MC=2
+1,MC=2 ![]() +
+ ![]() ,
,
∴点M的坐标为( ![]() +1,2
+1,2 ![]() +
+ ![]() ).
).
【解析】(1)由A、B两点的坐标,利用待定系数法可求得抛物线解析式;(2)分D在x轴上和y轴上,当D在x轴上时,过A作AD⊥x轴,垂足D即为所求;当D点在y轴上时,设出D点坐标为(0,d),可分别表示出AD、BD,再利用勾股定理可得到关于d的方程,可求得d的值,从而可求得满足条件的D点坐标;(3)过P作PF⊥CM于点F,利用Rt△ADO∽Rt△MFP以及三角函数,可用PF分别表示出MF和NF,从而可表示出MN,设BC=a,则可用a表示出CN,再利用S△BCN=2S△PMN , 可用PF表示出a的值,从而可用PF表示出CN,可求得 ![]() 的值;借助a可表示出M点的坐标,代入抛物线解析式可求得a的值,从而可求出M点的坐标.
的值;借助a可表示出M点的坐标,代入抛物线解析式可求得a的值,从而可求出M点的坐标.
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案