题目内容
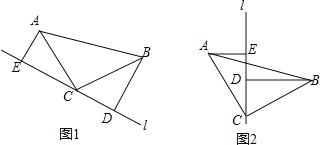
【题目】如图,△ABC中,∠ACB=90°,AC=BC,直线l过点C,BD⊥l,AE⊥l,垂足分别为D、E.
(1)当直线l不与底边AB相交时,求证:ED=AE+BD;
(2)如图2,将直线l绕点C顺时针旋转,使l与底边AB相交时,请你探究ED、AE、BD三者之间的数量关系.
【答案】(1)证明见解析;
(2)ED=BD﹣AE,理由见解析.
【解析】(1)根据垂直定义求出∠AEC=∠BDC=90°,求出∠EAC+∠ACE=90°,
∠EAC+∠ACE=90°,得∠EAC=∠BCD,根据AAS推出△AEC≌△CDB,再根据全等三角形的性质推出CE=BD和AE=CD即可;(2)同(1)可得证.
解:(1)∵直线l过点C,BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中,
∠EAC=∠BCD,∠AEC=∠BDC,AC=BC,
∴△AEC≌△CDB(AAS),
∴CE=BD,AE=CD,
∵ED=CE+CD,
∴ED=AE+BD;
(2)ED=BD﹣AE,
理由是:∵直线l过点C,BD⊥l,AE⊥l,
∴∠AEC=∠BDC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,
∴∠EAC=∠BCD,
在△AEC和△CDB中,
∠EAC=∠BCD,∠AEC=∠BDC,AC=BC,
∴△AEC≌△CDB(AAS),
∴CE=BD,AE=CD,
∵ED=CE﹣CD,
∴ED=BD﹣AE.

【题目】下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 若用电量为8千瓦时,则应交电费4.4元
D. y是x的反比例函数