题目内容
如图a,△ABC和△CEF是两个大小不等的等边三角形,且有一公共顶点C,连接AF和BE.
(1)线段AF和BE有怎样的大小关系?请证明你的结论;
(2)将图a中的△CEF绕点C顺时针旋转一定的角度,得到图b,(1)中的结论还成立吗?作出判断并说明 理由;
(3)若将图a中的△ABC绕点C逆时针旋转一定的角度,请你画一个变换后的图形c(草图即可),(1)中的结论还成立吗?作出判断不必说明理由;
(4)根据以上证明、说理、画图,归纳你的结论.
(1)线段AF和BE有怎样的大小关系?请证明你的结论;
(2)将图a中的△CEF绕点C顺时针旋转一定的角度,得到图b,(1)中的结论还成立吗?作出判断并说明 理由;
(3)若将图a中的△ABC绕点C逆时针旋转一定的角度,请你画一个变换后的图形c(草图即可),(1)中的结论还成立吗?作出判断不必说明理由;
(4)根据以上证明、说理、画图,归纳你的结论.

解:AF=BE,理由:
(1) ∵△ABC,△ECF都是等边三角形,
∴AC=BC,CF=CE, ACB=
ACB= BCE.
BCE.
在△ACF与△BCE中,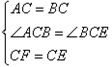
∴△ACF≌△BCE( SAS),
∴AF= BE.
(2)(1)中的结论仍成立,
∵ ACF+
ACF+ FCB =60°.
FCB =60°.
又∵ FCB+
FCB+  BCE =60°,
BCE =60°,
∴ ACF=
ACF= BCE.
BCE.
在△ACF与△BCE中,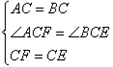
∴△ACF≌△BCE(SAS),
即AF= BE.
(3)如图,(1)中的结论仍成立.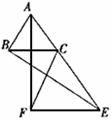 (4)根据以上证明、说明、画图,归纳如下:
(4)根据以上证明、说明、画图,归纳如下:
如图a,大小不等的等边三角形ABC和等边三角形CEF有且仅有一个公共顶点C,则以点C为旋转中心,任意旋转其中一个三角形,都有AF=BE。
(1) ∵△ABC,△ECF都是等边三角形,
∴AC=BC,CF=CE,
 ACB=
ACB= BCE.
BCE.在△ACF与△BCE中,
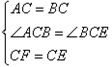
∴△ACF≌△BCE( SAS),
∴AF= BE.
(2)(1)中的结论仍成立,
∵
 ACF+
ACF+ FCB =60°.
FCB =60°.又∵
 FCB+
FCB+  BCE =60°,
BCE =60°, ∴
 ACF=
ACF= BCE.
BCE.在△ACF与△BCE中,
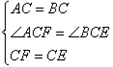
∴△ACF≌△BCE(SAS),
即AF= BE.
(3)如图,(1)中的结论仍成立.

如图a,大小不等的等边三角形ABC和等边三角形CEF有且仅有一个公共顶点C,则以点C为旋转中心,任意旋转其中一个三角形,都有AF=BE。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 15、如图,在△ABC和△DEF中,已知AB=DE,AC=DF,要使△ABC≌△DEF,根据三角形全等的判定公理还需添加条件(填上你认为正确的一种情况)
15、如图,在△ABC和△DEF中,已知AB=DE,AC=DF,要使△ABC≌△DEF,根据三角形全等的判定公理还需添加条件(填上你认为正确的一种情况)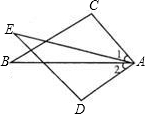 如图:在△ABC和△ADE中,已知∠1=∠2,∠B=∠E,AC=AD.请说明△ABC≌△AED的理由.
如图:在△ABC和△ADE中,已知∠1=∠2,∠B=∠E,AC=AD.请说明△ABC≌△AED的理由.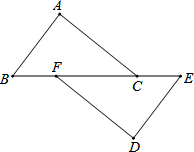 (2013•上海)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是
(2013•上海)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 如图,在△ABC和△ADE中,∠DAB=∠EAC,∠C=∠E.
如图,在△ABC和△ADE中,∠DAB=∠EAC,∠C=∠E. 如图,在△ABC和△EFD中,AB=EF,AC=ED,点B,D,C,F在一条直线上.
如图,在△ABC和△EFD中,AB=EF,AC=ED,点B,D,C,F在一条直线上.