题目内容
【题目】实践探究，解决问题
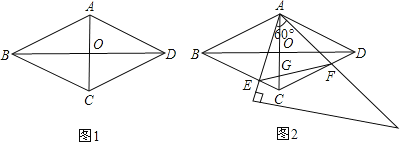
如图1，△ABC中，AD为BC边上的中线，则S△ABD=S△ACD ． 
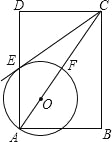
（1）在图2中，E、F分别为矩形ABCD的边AD、BC的中点，且AB=4，AD=8，则S阴影=；
（2）在图3中，E、F分别为平行四边形ABCD的边AD、BC的中点，则S阴影和S平行四边形ABCD之间满足的关系式为；
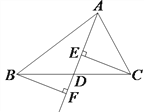
（3）在图4中，E、F分别为任意四边形ABCD的边AD、BC的中点，则S阴影和S四边形ABCD之间还满足（2）中的关系式吗？若满足，请予以证明，若不满足，说明理由．
解决问题：
（4）在图5中，E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点，并且图中阴影部分的面积为20平方米，求图中四个小三角形的面积和（即S1+S2+S3+S4的值）．
【答案】
（1）16
（2）S阴影= 
S平行四边形ABCD
（3）
解：满足（2）中的关系式，理由如下：
连接BD，由图1得S△EBD= S△ABD 同理S△BDF= S△BDC
∴S四边形EBFD=S△EBD+S△BDF= S四边形ABCD
（4）
解：设四边形的空白区域分别为a，b，c，d
由上述性质可以得出：
a+S2+S3= S△ACD①，c+S1+S4= S△ACB②，b+S2+S1= S△ABD③，d+S4+S3= S△ACD④，
①+②+③+④得，a+S2+S3+c+S1+S4+b+S2+S1+d+S4+S3=S四边形ABCD⑤
而S四边形ABCD=a+b+c+d+S1+S2+S3+S4+S阴影⑥
所以联立⑤⑥得S1+S2+S3+S4=S阴影=20平方米．
【解析】解：（1）∵E、F分别为矩形ABCD的边AD、BC的中点，且AB=4，AD=8，
∴S阴影= ×8×4=16，
所以答案是：16；（2）∵E、F分别为平行四边形ABCD的边AD、BC的中点，
∴S阴影= S平行四边形ABCD；
所以答案是：S阴影= S平行四边形ABCD；
【考点精析】本题主要考查了矩形的性质的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等才能正确解答此题．
