ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏΨ≠ΙΐΒψAΘ®©¹3Θ§0Θ©Θ§FΘ®8Θ§0Θ©Θ§BΘ®0Θ§4Θ©»ΐΒψ
Θ®1Θ©«σ≈ΉΈοœΏΫβΈω ΫΦΑΕ‘≥Τ÷αΘΜ
Θ®2Θ©»τΒψD‘ΎœΏΕΈFB…œ‘ΥΕ·Θ®≤Μ”κFΘ§B÷ΊΚœΘ©Θ§ΙΐΒψDΉςDCΓΆ÷α”ΎΒψCΘ®xΘ§0Θ©Θ§ΫΪΓςFCD―ΊCDœρΉσΖ≠’έΘ§ΒψBΕ‘”ΠΒψΈΣΒψEΘ§ΓςCDE”κΓςFBO÷ΊΒΰ≤ΩΖ÷ΟφΜΐΈΣSΘ°
ΔΌ ‘«σ≥ωS”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩ»Γ÷ΒΖΕΈßΘ°
ΔΎ «Ζώ¥φ‘Ύ’β―υΒΡΒψCΘ§ ΙΒΟΓςBDEΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§»τ¥φ‘ΎΘ§«σ≥ωCΒψΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©≈ΉΈοœΏΕ‘≥Τ÷α…œ”–“ΜΒψMΘ§ΤΫΟφΡΎ”–“ΜΒψNΘ§»τ“‘AΘ§BΘ§MΘ§NΥΡΒψΉι≥…ΒΡΥΡ±Ώ–ΈΈΣΝβ–ΈΘ§«σΒψNΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©
ΫβΘΚ…η≈ΉΈοœΏΫβΈω ΫΈΣy=aΘ®x+3Θ©Θ®x©¹8Θ©Θ§
ΫΪΒψBΘ®0Θ§4Θ©¥ζ»κΒΟ4=aΓΝΘ®0+3Θ©ΓΝΘ®0©¹8Θ©Θ§
ΫβΒΟa=©¹ ![]() Θ°
Θ°
Ι ≈ΉΈοœΏΫβΈω ΫΈΣy=©¹ ![]() Θ®x+3Θ©Θ®x©¹8Θ©Θ§
Θ®x+3Θ©Θ®x©¹8Θ©Θ§
Ε‘≥Τ÷αΈΣx=Θ®©¹3+8Θ©Γ¬2= ![]() ΘΜ
ΘΜ
Θ®2Θ©
ΫβΘΚCE=CF=8©¹xΘ§CD=4©¹ ![]() xΘ§
xȧ
ΔΌΒ±0ΘΦxΘΦ4 ±Θ§
S= ![]() Θ®8©¹xΘ©Θ®4©¹
Θ®8©¹xΘ©Θ®4©¹ ![]() xΘ©ΓΝ[1©¹Θ®
xΘ©ΓΝ[1©¹Θ® ![]() Θ©2]=©¹
Θ©2]=©¹ ![]() x2+4xΘΜ
x2+4xΘΜ
Β±4ΓήxΘΦ8 ±Θ§
S= ![]() Θ®8©¹xΘ©Θ®4©¹
Θ®8©¹xΘ©Θ®4©¹ ![]() xΘ©=
xΘ©= ![]() x2©¹4x+16ΘΜ
x2©¹4x+16ΘΜ
ΔΎΖ÷ΝΫ÷÷«ιΩωΘΚΒ±ΓœBED=90Γψ ±Θ§ΓςBOEΓΉΓςECDΘ§
Γύ ![]() =
= ![]() =2Θ§
=2Θ§
ΓύEC=3Θ§
ΓύC1Θ®5Θ§0Θ©ΘΜ
Β±ΓœEBD=90Γψ ±ΘΜ
ΓςEOBΓΉΓςBOFΘ§
Γύ ![]() =
= ![]() =2Θ§
=2Θ§
ΓύEO=2Θ§
ΓύEC= ![]() =5Θ§
=5Θ§
ΓύC2Θ®3Θ§0Θ©ΘΜ
Θ®3Θ©
ΫβΘΚΔΌ“‘ABΈΣ±ΏΘ§“‘BΈΣ‘≤–ΡΘ§ABΈΣΑκΨΕΜ≠‘≤ΫΜΕ‘≥Τ÷α”ΎM1Θ§M2ΝΫΒψΘ§
M1I= ![]() =
= ![]() Θ§
Θ§
”…BM1Θ§ΤΫ“Τ÷ΝAN1ΒΟΘ§N1Θ®©¹ ![]() Θ§
Θ§ ![]() Θ©Θ§N2Θ®©¹
Θ©Θ§N2Θ®©¹ ![]() Θ§©¹
Θ§©¹ ![]() Θ©Θ§
Θ©Θ§
“‘AΈΣ‘≤–ΡΘ§ABΈΣΑκΨΕΜ≠‘≤Θ§¥Υ ±”κΕ‘≥Τ÷αΟΜ”–ΫΜΒψΘ§Ι ≤Μ¥φ‘ΎΘΜ
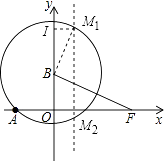
ΔΎ“‘ABΈΣΕ‘Ϋ«œΏΘ§÷±œΏABΒΡΫβΈω ΫΈΣΘΚy= ![]() x+4Θ§
x+4Θ§
‘ρABΒΡ÷–¥ΙœΏMNΒΡΫβΈω ΫΈΣΘΚy=©¹ ![]() x+
x+ ![]() Θ§
Θ§
Β±x= ![]() ±Θ§y=©¹1Θ§
±Θ§y=©¹1Θ§
ΓύMΘ® ![]() Θ§©¹1Θ©Θ§
Θ§©¹1Θ©Θ§
ΓύN3Θ®©¹ ![]() Θ§5Θ©Θ°
Θ§5Θ©Θ°
Ήέ…œΥυ ωΘΚN1Θ®©¹ ![]() Θ§
Θ§ ![]() Θ©Θ§N2Θ®©¹
Θ©Θ§N2Θ®©¹ ![]() Θ§©¹
Θ§©¹ ![]() Θ©Θ§N3Θ®©¹
Θ©Θ§N3Θ®©¹ ![]() Θ§5Θ©Θ°
Θ§5Θ©Θ°
ΓΨΫβΈωΓΩΘ®1Θ©Ω……η≈ΉΈοœΏΫβΈω ΫΈΣy=aΘ®x+3Θ©Θ®x©¹8Θ©Θ§ΫΪΒψBΘ®0Θ§4Θ©¥ζ»κ“―÷Σ≈ΉΈοœΏΖΫ≥ΧΘ§ΫβΒΟaΒΡ÷ΒΦ¥Ω…ΘΜΘ®2Θ©ΔΌΖ÷ΝΫ÷÷«ιΩωΘΚ0ΘΦxΘΦ4ΘΜ4ΓήxΘΦ8ΘΜΫχ––Χ÷¬έΩ…«σS”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜΔΎΖ÷ΝΫ÷÷«ιΩωΘΚΒ±ΓœBED=90Γψ ±ΘΜΒ±ΓœEBD=90Γψ ±ΘΜΫχ––Χ÷¬έΩ…«σCΒψΉχ±ξΘΜΘ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΘΚΔΌ“‘ABΈΣ±ΏΘ§“‘BΈΣ‘≤–ΡΘ§ABΈΣΑκΨΕΜ≠‘≤ΫΜΕ‘≥Τ÷α”ΎM1 Θ§ M2ΝΫΒψΘΜΔΎ“‘ABΈΣΕ‘Ϋ«œΏΘΜΫχ––Χ÷¬έΩ…«σΒψNΒΡΉχ±ξΘ°

ΓΨΧβΡΩΓΩΡ≥–ΘΚœ≥ΣΆ≈”–30Οϊ≥…‘±Θ§œ¬±μ «Κœ≥ΣΆ≈≥…‘±ΒΡΡξΝδΖ÷≤ΦΆ≥ΦΤ±μΘΚ
ΡξΝδΘ®ΒΞΈΜΘΚΥξΘ© | 13 | 14 | 15 | 16 |
ΤΒ ΐΘ®ΒΞΈΜΘΚΟϊΘ© | 5 | 15 | x | 10©¹x |
Ε‘”Ύ≤ΜΆ§ΒΡxΘ§œ¬Ν–ΙΊ”ΎΡξΝδΒΡΆ≥ΦΤΝΩ≤ΜΜαΖΔ…ζΗΡ±δΒΡ «Θ® Θ©
A.ΤΫΨυ ΐΓΔ÷–ΈΜ ΐ
B.ΤΫΨυ ΐΓΔΖΫ≤ν
C.÷Ύ ΐΓΔ÷–ΈΜ ΐ
D.÷Ύ ΐΓΔΖΫ≤ν
ΓΨΧβΡΩΓΩΡ≥…Χ≥ΓΆΕ»κ13800‘ΣΉ ΫπΙΚΫχΦΉΓΔ““ΝΫ÷÷Ωσ»ΣΥ°Ι≤500œδΘ§Ωσ»ΣΥ°ΒΡ≥…±ΨΦέΚΆœζ έΦέ»γ±μΥυ ΨΘΚ
άύ±π/ΒΞΦέ | ≥…±ΨΦέ | œζ έΦέΘ®‘Σ/œδΘ© |
ΦΉ | 24 | 36 |
““ | 33 | 48 |
Θ®1Θ©ΗΟ…Χ≥ΓΙΚΫχΦΉΓΔ““ΝΫ÷÷Ωσ»ΣΥ°ΗςΕύ…ΌœδΘΩ
Θ®2Θ©»Ϊ≤Ω έΆξ500œδΩσ»ΣΥ°Θ§ΗΟ…Χ≥ΓΙ≤ΜώΒΟάϊ»σΕύ…Ό‘ΣΘΩ