题目内容
【题目】一艘轮船以每小时20千米的速度从甲港驶往160千米远的乙港,2小时后,一艘快艇以每小时40千米的速度也从甲港驶往乙港.分别列出轮船和快艇行驶的路程y(千米)与时间x(小时)的函数关系式,在下图中的直角坐标系中画出函数图象,观察图象回答下列问题:
(1)何时轮船行驶在快艇的前面?
(2)何时快艇行驶在轮船的前面?
(3)哪一艘船先驶过60千米?哪一艘船先驶过100千米?
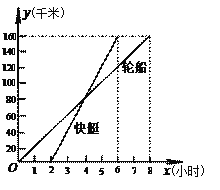
【答案】(1)x<4小时时(2)4小时后(3)轮船先驶过60千米,快艇先驶过100千米.
【解析】试题分析:运用待定系数法分别求函数关系式;解方程组求交点坐标,结合图象回答(1)、(2)两个问题;(3)直接观察图象即可回答即可.
解:设快艇的函数关系式为y1=kx+b.
∵图象过(2,0)、(6,160),
∴![]() ,
,
解得![]() .
.
∴y1=40x-80.
同理可求轮船的函数关系式为y2=20x.
当y1=y2时,40x-80=20x,解得 x=4.
即x=4时,快艇追上轮船.
观察图象可知:
(1)轮船行使4小时之前,轮船行驶在快艇的前面;
(2)轮船行使4小时之后,快艇行驶在轮船的前面;
(3)轮船先驶过60千米,快艇先驶过100千米.

练习册系列答案
相关题目