题目内容
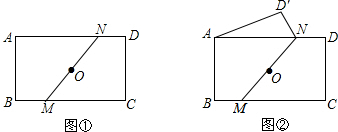
已知在矩形ABCD中,AD>AB,O为对角线的交点,过O作一直线分别交BC、AD于M、N.
(1)如图①,求证:梯形ABMN的面积等于梯形CDNM的面积;
(2)如图②,若矩形ABCD沿MN折叠,能使得点C与点A重合,且翻折后不重叠部分的面积是重叠部分的面积的
,求BM:MC的值;
(3)矩形ABCD沿MN折叠,当MN满足 时,才能使得点C恰好与点A重合(只写出结果,不要求证明).
(1)如图①,求证:梯形ABMN的面积等于梯形CDNM的面积;
(2)如图②,若矩形ABCD沿MN折叠,能使得点C与点A重合,且翻折后不重叠部分的面积是重叠部分的面积的
| 1 | 2 |
(3)矩形ABCD沿MN折叠,当MN满足

分析:(1)连接AC,根据矩形的对角线互相平分可得AO=CO,再根据两直线平行,内错角相等可得∠MCO=∠ANO,然后利用“角边角”证明△AON和△COM全等,根据全等三角形对应边相等可得AN=CM,再求出BM=DN,然后根据梯形的面积公式证明即可;
(2)连接AM,根据翻折的性质可得AM=MC,AD′=CD,∠AMN=∠CMN,再根据两直线平行,内错角相等可得∠ANM=∠CMN,然后求出∠AMN=∠ANM,根据等角对等边可得AM=AN,利用“HL”证明△ABM和△AD′N全等,根据全等三角形的面积相等可得S△AD′N=S△ABM,再根据三角形的面积求出BM=
AN,然后求解即可;
(3)根据翻折的性质,MN与AC互相垂直时点C与A重合.
(2)连接AM,根据翻折的性质可得AM=MC,AD′=CD,∠AMN=∠CMN,再根据两直线平行,内错角相等可得∠ANM=∠CMN,然后求出∠AMN=∠ANM,根据等角对等边可得AM=AN,利用“HL”证明△ABM和△AD′N全等,根据全等三角形的面积相等可得S△AD′N=S△ABM,再根据三角形的面积求出BM=
| 1 |
| 2 |
(3)根据翻折的性质,MN与AC互相垂直时点C与A重合.
解答:(1)证明:如图,连接AC,∵O为对角线的交点,
∴AO=CO,
∵矩形ABCD的边AD∥BC,
∴∠MCO=∠ANO,
在△AON和△COM中,
,
∴△AON≌△COM(ASA),
∴AN=CM,
∵AD=BC,
AN+DN=AD,BM+CM=BC,
∴BM=DN,
∵梯形ABMN的面积=
(AN+BM)•AB,
梯形CDNM的面积=
(DN+CM)•CD,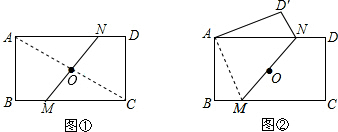
∴梯形ABMN的面积等于梯形CDNM的面积;
(2)如图,连接AM,∵矩形ABCD沿MN折叠,点C与点A重合,
∴AM=MC,AD′=CD,∠AMN=∠CMN,
∵AD∥BC,
∴∠ANM=∠CMN,
∴∠AMN=∠ANM,
∴AM=AN,
在△ABM和△AD′N中,
,
∴△ABM≌△AD′N(HL),
∴S△AD′N=S△ABM,
∵翻折后不重叠部分的面积是重叠部分的面积的
,
∴
AB•BM=
×
AN•AB,
∴BM=
AN,
∵AM=MC=AN,
∴BM:MC=1:2;
(3)当MN满足MN⊥AC时,才能使得点C恰好与点A重合.
故答案为:MN⊥AC.
∴AO=CO,
∵矩形ABCD的边AD∥BC,
∴∠MCO=∠ANO,
在△AON和△COM中,
|
∴△AON≌△COM(ASA),
∴AN=CM,
∵AD=BC,
AN+DN=AD,BM+CM=BC,
∴BM=DN,
∵梯形ABMN的面积=
| 1 |
| 2 |
梯形CDNM的面积=
| 1 |
| 2 |

∴梯形ABMN的面积等于梯形CDNM的面积;
(2)如图,连接AM,∵矩形ABCD沿MN折叠,点C与点A重合,
∴AM=MC,AD′=CD,∠AMN=∠CMN,
∵AD∥BC,
∴∠ANM=∠CMN,
∴∠AMN=∠ANM,
∴AM=AN,
在△ABM和△AD′N中,
|
∴△ABM≌△AD′N(HL),
∴S△AD′N=S△ABM,
∵翻折后不重叠部分的面积是重叠部分的面积的
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴BM=
| 1 |
| 2 |
∵AM=MC=AN,
∴BM:MC=1:2;
(3)当MN满足MN⊥AC时,才能使得点C恰好与点A重合.
故答案为:MN⊥AC.
点评:本题考查了翻折变换的性质,全等三角形的判定与性质,矩形的性质,等角对等边的性质,以及平行线的性质,熟记翻折前后的两个图形能够完全重合得到相等的边和角是解题的关键.

练习册系列答案
相关题目
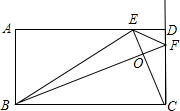 ,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).
,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).
 (2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.
(2012•德庆县一模)如图,已知在矩形ABCD中,E是AD上的一点,连接EC,BC=CE,BF⊥EC于点F.