Question

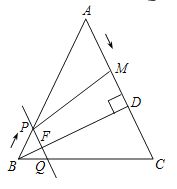
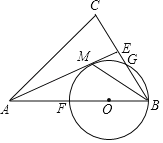
【题目】已知：如图，在△ABC中，AB＝AC，AE是∠CAB的角平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．

（1）求证：AE与⊙O相切；

（2）当BC＝6，cosC＝，求⊙O的半径．

Answer 1

【答案】（1）详见解析；（2）⊙O的半径为．

【解析】

（1）连接OM，证出∠EBM＝OMB，得出OM∥BE；由等腰三角形的性质，得AE⊥BC，则OM⊥AE，从而证明结论；

（2）设⊙O的半径是r，根据等腰三角形三线合一的性质，得BE＝CE＝3，解直角三角形求得AB＝AC＝5，则OA＝5﹣r，从而根据平行线分线段成比例定理求解．

（1）证明：连接OM，

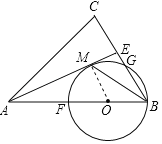
∵OB＝OM，

∴∠OBM＝∠OMB．

∵BM平分∠ABC，

∴∠OBM＝∠EBM，

∴∠EBM＝∠OMB，

∴OM∥BE．

∵AB＝AC，AE是∠CAB的平分线，

∴AE⊥BC，

∴OM⊥AE，

∴AE与⊙O相切；

（2）解：设⊙O的半径是r．

∵AB＝AC，AE是∠CAB的角平分线，，

∴AE⊥BC，BE＝CE＝3，∠ABC＝∠C．

∵，

∴AB＝AC＝＝＝5，

则OA＝5﹣r．

∵OM∥BE，

∴＝，

即＝，

解得r＝，

即⊙O的半径为．