Question

已知：在平面直角坐标系中，△ABC的顶点A、C分别在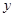轴、轴上，且∠ACB=90°,AC=BC.
（1）如图1，当，点B在第四象限时，则点B的坐标为      
（2）如图2，当点C在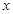轴正半轴上运动，点A在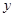轴正半轴上运动，点B在第四象限时，作BD⊥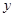轴于点D，试判断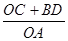与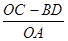哪一个是定值，并说明定值是多少？请证明你的结论.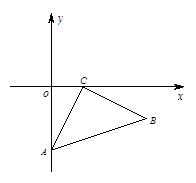

Answer 1

(1)点B的坐标为（  3，－1 ）    
（2）结论：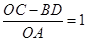      
证明：作BE⊥轴于E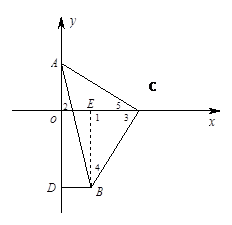       

∴∠1=90º=∠2
∴∠3+∠4=90º
∵∠ACB=90º
∴∠5+∠3=90º
∴∠5=∠4
在△CEB和△AOC中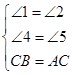

∴△CEB≌△AOC
∴AO=CE,   
∵BE⊥轴于E
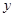∴BE∥轴
∵BD⊥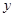轴于点D，E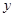O⊥轴于点O
∴EO=BD   
∴OC－BD=OC－EO=CE=AO
∴      

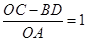
解析