题目内容
【题目】如图,在直角坐标系中,点P的坐标为(2,0),⊙P与x轴相交于原点O和点A,又B、C两点的坐标分别为(0,b),(﹣1,0).
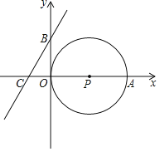
(1)当b=2时,求经过B、C两点的直线解析式;
(2)当B点在y轴上运动时,直线BC与⊙P位置关系如何?并求出相应位置b的值
【答案】(1)y=2x+2;(2)当b=±![]() 时,直线BC与⊙P相切;当b>
时,直线BC与⊙P相切;当b>![]() 或b<﹣
或b<﹣![]() 时,直线BC与⊙P相离;当﹣
时,直线BC与⊙P相离;当﹣![]() <b<
<b<![]() 时,直线BC与⊙P相交.
时,直线BC与⊙P相交.
【解析】
(1)由待定系数法求一次函数解析式;
(2)分直线BC与⊙O相切,相交,相离三种情况讨论,可求b的取值范围.
解:(1)设BC直线的解析式:y=kx+b
由题意可得: ![]()
∴解得:k=2,b=2
∴BC的解析式为:y=2x+2
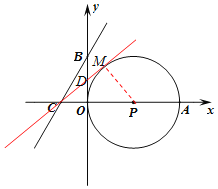
(2)设直线BC在x轴上方与⊙P相切于点M,交y轴于点D,连接PM,则PM⊥CM.
在Rt△CMP和Rt△COD中,
CP=3,MP=2,OC=1,CM=![]()
∵∠MCP=∠OCD
∴tan∠MCP=tan∠OCP
∴![]() =
=![]() ,b=OD=
,b=OD=![]() ×1=
×1=![]()
由轴对称性可知:b=±![]()
∴当b=±![]() 时,直线BC与⊙P相切;
时,直线BC与⊙P相切;
当b>![]() 或b<﹣
或b<﹣![]() 时,直线BC与⊙P相离;
时,直线BC与⊙P相离;
当﹣![]() <b<
<b<![]() 时,直线BC与⊙P相交.
时,直线BC与⊙P相交.

练习册系列答案
相关题目