Question

【题目】在平面直角坐标系中，将函数y＝2x2＋2的图象绕坐标原点0顺时针旋转45°后，得到新曲线l.

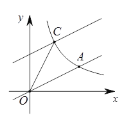
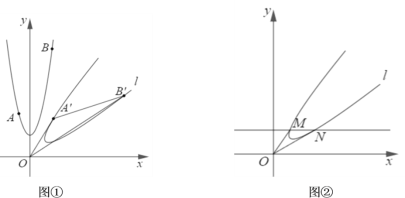
(1)如图①，已知点A(-1，a)，B(b，10)在函数y＝2x2＋2的图象上，若A’、B’是A、B旋转后的对应点，连结OA’，OB’，则S△OA’B’=____.

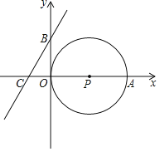
(2)如图②，曲线与直线相交于点M、N，则S△OMN为_________.

Answer 1

【答案】9

【解析】

（1）如图③，连结OA、OB、AB，则由旋转的性质可知S△OA’B’=S△OAB.根据题意求出A,B坐标，构造三角形即可求出S△OAB.

（2）先画出图形，根据旋转的性质，可知S△OMN=S△OM’N’.由题意可知直线M’ N’的解析式为y=x+3，从而求出M’ ，N’的横坐标分别为、1，得出直线M’ N’与y轴的交点记为C，其坐标为(0，3)，即可得出S△OAB.

(1)如图③，连结OA、OB、AB，则由旋转的性质可知S△OA’B’=S△OAB.

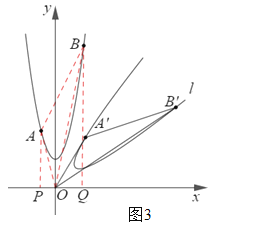
由A、B在函数y＝2x2＋2的图象上，可求得A(-1，4)、B(2，10).

分别过点A、B作x轴的垂线，垂足分别记为P、Q，则有：

S△OAB=S梯形APQB-S△PAO-S△QBO=×（4+10）×3-×1×4-×2×10=9.

(2)将曲线l、直线和△OMN绕着原点O逆时针旋转45°，旋转之后的图象如图④所示: △OMN旋转到△OM’ N’的位置，直线旋转到直线M’ N’的位置.

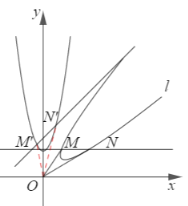
图④

根据旋转的性质，可知S△OMN= S△OM’N’.

直线MN与y轴的交点 (0,)经过旋转之后，其坐标变为(-,)，显然该点在直线M’ N’.

而直线M’ N’的斜率为1，易求得直线M’ N’的解析式为y=x+3.

令2x2+2=x+3，整理得2x2-x-1=0，解得x=1或，即M’ 、N’的横坐标分别为、1.

直线M’ N’与y轴的交点记为C，其坐标为(0，3).

故S△OMN= S△OM’N’=OC=×3×=.