题目内容
【题目】定义:在平面直角坐标系中,如果点![]() 到直线
到直线![]() 的距离与它到
的距离与它到![]() 轴、
轴、![]() 轴的距离都相等,那么称点
轴的距离都相等,那么称点![]() 为直线
为直线![]() 的“稳定点”.
的“稳定点”.
(1)到![]() 轴、
轴、![]() 轴的距离相等的点一定在直线__________________上;
轴的距离相等的点一定在直线__________________上;
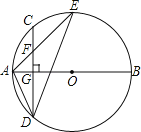
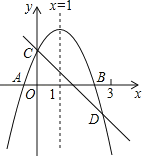
(2)在下图中作出直线![]() ,并求出该直线所有“稳定点”的坐标;
,并求出该直线所有“稳定点”的坐标;
(备用图)
(3)当![]() 时,直线
时,直线![]() 的“稳定点”
的“稳定点”![]() 的坐标为__________________;
的坐标为__________________;
(4)当![]() 时,直线
时,直线![]() 的所有“稳定点”的横坐标之间存在何种数量关系,请画图直接说明,无需证明.
的所有“稳定点”的横坐标之间存在何种数量关系,请画图直接说明,无需证明.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ,
,![]() ;(3)
;(3)![]() 或
或![]() ;(4)见解析
;(4)见解析
【解析】
(1)由题意可得,点P的横、纵坐标相等或互为相反数,从而求出结论;
(2)点P即为直线y=x与∠BAO的角平分线的交点或直线y=x与
![]() 的邻补角的角平分线的交点或直线y=-x与∠BAO的角平分线的交点或直线y=-x与
的邻补角的角平分线的交点或直线y=-x与∠BAO的角平分线的交点或直线y=-x与![]() 的邻补角的角平分线的交点,求出直线AC的解析式和第二条角平分线所在直线的解析式即可得出结论;
的邻补角的角平分线的交点,求出直线AC的解析式和第二条角平分线所在直线的解析式即可得出结论;
(3)求出直线![]() 与直线y=x 的交点或直线
与直线y=x 的交点或直线![]() 与直线y=-x 的交点即可得出结论;
与直线y=-x 的交点即可得出结论;
(4)记四个“稳定点”的横坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() ,设P1、P3在直线y=x上P2、P4在y=-x上,
,设P1、P3在直线y=x上P2、P4在y=-x上,![]() >0,
>0,![]() >0,
>0,![]() >0,
>0,![]() <0,如图所示,根据相似三角形的判定及性质即可得出结论.
<0,如图所示,根据相似三角形的判定及性质即可得出结论.
解:(1)由题意可得,点P的横、纵坐标相等或互为相反数
∴到![]() 轴、
轴、![]() 轴的距离相等的点一定在直线
轴的距离相等的点一定在直线![]() 或直线
或直线![]()
故答案为:![]() 或
或![]() ;
;
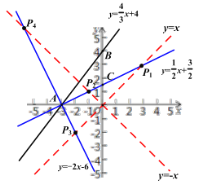
(2)如图,由题意可得:点P即为直线y=x与∠BAO的角平分线的交点或直线y=x与![]() 的邻补角的角平分线的交点或直线y=-x与∠BAO的角平分线的交点或直线y=-x与
的邻补角的角平分线的交点或直线y=-x与∠BAO的角平分线的交点或直线y=-x与![]() 的邻补角的角平分线的交点
的邻补角的角平分线的交点
直线![]() 与x轴的交点坐标为(-3,0),与y轴的交点坐标为(0,4)
与x轴的交点坐标为(-3,0),与y轴的交点坐标为(0,4)
∴OA=3,OB=4
根据勾股定理可得AB=![]()
作出![]() 的角平分线
的角平分线![]() ,交
,交![]() 轴于点
轴于点![]() .
.
利用角平分线的性质可得△ABC的边AB上的高的长即为OC的长
∵S△ABO=S△ABC+S△OAC
∴![]() OA·OB=
OA·OB=![]() AB·OC+
AB·OC+![]() OA·OC
OA·OC
即![]() ×3×4=
×3×4=![]() ×5·OC+
×5·OC+![]() ×3·OC
×3·OC
解得:OC=![]()
∴点C的坐标为(0,![]() )
)
设直线![]() 的解析式为
的解析式为![]()
将点A和点C的坐标代入,可得
直线![]() 的解析式为
的解析式为![]() ;
;
再作出![]() 的邻补角的角平分线,
的邻补角的角平分线,
同样可求第二条角平分线所在直线的解析式为![]() .
.
故联立组成方程组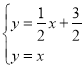 、
、 、
、![]() 、
、![]() 得“稳定点”的
得“稳定点”的![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(3)由题意可得:当![]() 时,直线
时,直线![]() 的“稳定点”应为直线
的“稳定点”应为直线![]() 与直线y=x 的交点或直线
与直线y=x 的交点或直线![]() 与直线y=-x 的交点
与直线y=-x 的交点
故联立组成方程组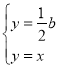 、
、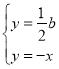
∴![]() 点的坐标为
点的坐标为![]() 或
或![]()
故答案为:![]() 或
或![]() ;
;
(4)如图,记四个“稳定点”的横坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() ,设P1、P3在直线y=x上P2、P4在y=-x上,
,设P1、P3在直线y=x上P2、P4在y=-x上,![]() >0,
>0,![]() >0,
>0,![]() >0,
>0,![]() <0,如图所示
<0,如图所示
∴P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() )
)
直线![]() 与x轴的交点C的坐标为(
与x轴的交点C的坐标为(![]() ,0)
,0)
过点P3作P3A⊥x轴于A,过点P2作P2B⊥x轴于B,P3P4与P1P2交于点C
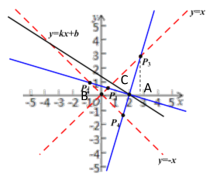
由(2)可知:两个角平分线互相垂直,即P3P4⊥P1P2,
易证△P3AC∽△CBP2
∴![]()
∴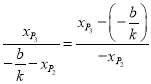
整理,得
![]()
∵b≠0
∴![]()
同理可得![]()
∴![]() .
.

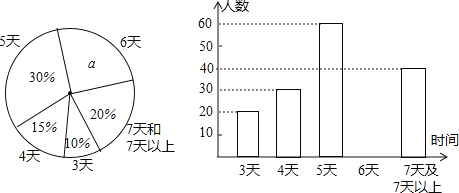
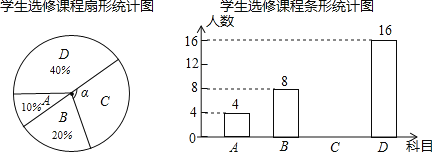
【题目】面对疫情,每个人都需要积极行动起来,做好预防工作.为此某校开展了“新型冠状病毒肺炎”防控知识竞赛.现从该校五、六年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:A.
表示,共分成四组:A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
五年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
六年级10名学生的竞赛成绩在C组中的数据是:94,90,94
五、六年级抽取的学生竞赛成绩统计表
年级 | 平均数 | 中位数 | 众数 | 方差 |
五年级 | 92 | 93 |
| 52 |
六年级 | 92 |
| 100 | 50.4 |
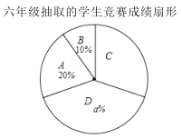
是据以上信息,解答下列问题:
(1)直接写出上述图表中![]() ,
,![]() ,
,![]() 的值:
的值:![]() __________,
__________,![]() ___________,
___________,![]() ___________;
___________;
(2)由以上数据,你认为该校五、六年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校五、六年级共1800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀![]() 的学生人数是多少?
的学生人数是多少?