题目内容
【题目】如图,已知⊙O的直径AB=6,E、F为AB的三等分点,M、N为 ![]() 上两点,且∠MEB=∠NFB=60°,则EM+FN= .
上两点,且∠MEB=∠NFB=60°,则EM+FN= . 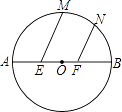
【答案】![]()
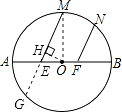
【解析】解:如图,延长ME交⊙O于G, ∵E、F为AB的三等分点,∠MEB=∠NFB=60°,
∴FN=EG,
过点O作OH⊥MG于H,连接MO,
∵⊙O的直径AB=6,
∴OE=OA﹣AE= ![]() ×6﹣
×6﹣ ![]() ×6=3﹣2=1,
×6=3﹣2=1,
OM= ![]() ×6=3,
×6=3,
∵∠MEB=60°,
∴OH=OEsin60°=1× ![]() =
= ![]() ,
,
在Rt△MOH中,MH= ![]() =
= ![]() =
= ![]() ,
,
根据垂径定理,MG=2MH=2× ![]() =
= ![]() ,
,
即EM+FN= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 名校课堂系列答案
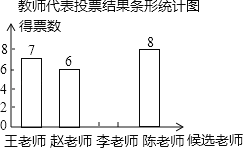
名校课堂系列答案【题目】为激励教师爱岗敬业,某市开展了“我最喜爱的老师”评选活动.某中学确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
候选教师 | 王老师 | 赵老师 | 李老师 | 陈老师 |
得票数 | 200 | 300 |
学生投票结果统计表
(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)王老师与李老师得到的学生总票数是500,且王老师得到的学生票数是李老师得到的学生票数的3倍多20票,求王老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?