题目内容
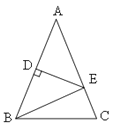
【题目】如图，△ABC中,AB=AC，DE垂直平分AB，D为垂足交AC于E.
（1）若∠A=50°，求∠EBC的度数；
（2）若
，△BEC的周长是11，求ABC的周长.
【答案】（1）15°；（2）19.
【解析】试题分析：（1）由等腰三角形的性质可求得∠ABC，由线段垂直平分线的性质可求得∠ABE，则可求得∠EBC；
（2）由线段垂直平分线的性质可求得BE+EC+BC=AE+EC+BC=AC+BC，再结合△BEC的周长，可求得BC的长，进一步得到△ABC的周长．
试题解析：（1）∵AB=AC，∠A=50°，
∴∠ABC=∠C=65°．
∵DE垂直平分AB，
∴AE=BE，
∴∠ABE=∠A=50°．
∴∠DBC=15°．
（2）∵AE=BE，AB=8，
∴BE+CE=8．
∵△BEC的周长是11，
∴BC=3，
∴△ABC的周长是8+8+3=19．
练习册系列答案
相关题目
