题目内容
【题目】如图,平行四边形ABCD的两个顶点坐标分别为A(1,3),B(3,3),对角线的交点为M(1,2),AD与y轴的交点为N.
(1)求C、D点的坐标;
(2)求证:△BCN的面积是平行四边形ABCD面积的一半;
(3)除了点N,坐标轴上是否存在点P,使△BCP的面积是平行四边形ABCD面积的一半,若存在,直接写出P点的坐标;若不存在,请说明理由.
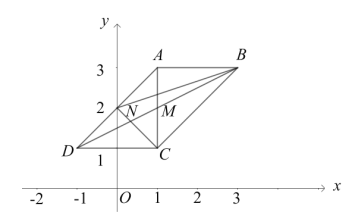
【答案】(1) C(1,1),D(-1,1);(2)见解析.(3) P点的坐标为(-2,0),(2,0)或(0,-2)
【解析】
(1)根据平行四边形的性质求出C,D两点的坐标;
(2)分别表示出△BCN的面积,平行四边形ABCD的面积,然后探究他们之间的大小关系;
(3)分三种情况进行分类讨论,P在y负半轴,在x正半轴,x负半轴分别进行讨论.
解:(1)∵A(1,3),B(3,3), M(1,2),
∴AB=2,AM=1,AB![]() x轴,AM⊥x轴,
x轴,AM⊥x轴,
∴A,C,M三点的横坐标相等为1,C,D两点的纵坐标相等.
∵四边形ABCD是平行四边形,M是平行四边形对角线的交点,
∴CD=AB=2,CD![]() AB,AM=CM=1
AB,AM=CM=1
∴C点的纵坐标为3-2=1,D点的横坐标为-1
∴C(1,1),D(-1,1).
(2)设A点到BC的距离为h,则平行四边形ABCD的面积为AB![]() h.
h.
∵四边形ABCD是平行四边形,
∴AD![]() BC
BC
∴点N到BC的距离为h
∴△BCN的面积为![]() BC
BC![]() h
h
∴△BCN的面积是平行四边形ABCD面积的一半.
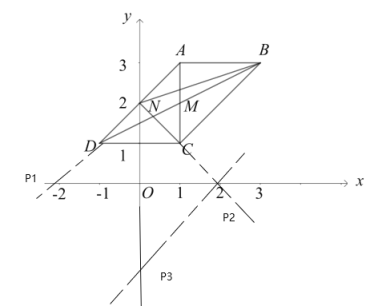
(3)根据平行线之间的距离相等,则延长AD交x轴与P1,有△BCP1的面积是平行四边形ABCD面积的一半.
设直线AD的解析式为y=kx+b,将A(1,3),D(-1,1)代入y=kx+b中,得
![]() 解得
解得![]()
∴直线AD的解析式为y=x+2
∴∠ADC=45°
当y=0时,x=-2
∴P1(-2,0)
当x=0时,y=2
∴N(0,2)
又∵C(1,1),D(-1,1),
∴NC=ND
∴∠NCD=∠ADC=45°
∴三角形NDC为等腰直角三角形,∠DNC=90°,∠ONC=45°
延长NC交x轴于点P2,则三角形NOP2是等腰直角三角形,所以OP2=ON=2
∴P2(2,0)
过P2作AD的平行线交y轴于P3,则P2 P3的解析式为y=x-2.
当x=0时,y=-2.
∴P3(0,-2)
则P点的坐标为(-2,0),(2,0)或(0,-2)时,△BCP的面积是平行四边形ABCD面积的一半.

 阅读快车系列答案
阅读快车系列答案