题目内容
【题目】△ABC和△DEF的顶点A与D重合,已知∠B=90°,∠BAC=30°,BC=6,∠FDE=90°,DF=DE=4.
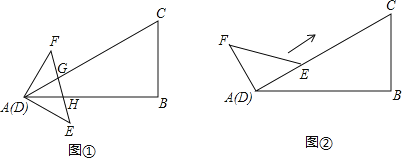
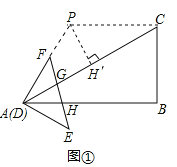
(1)如图①,EF与边AC、AB分别交于点G、H,且FG=EH.设![]() ,在射线DF上取一点P,记:
,在射线DF上取一点P,记: ![]() ,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
(2)在(1)的条件下,求当x为何值时PC//AB;
(3)如图②,先将△DEF绕点D逆时针旋转,使点E恰好落在AC边上,在保持DE边与AC边完全重合的条件下,使△DEF沿着AC方向移动![]() 当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 移动到AD=
移动到AD=![]() 时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
【解析】试题分析:(1)首先证明△DFG≌△DEH(SAS),进而得出∠FDG=∠EDH,进而得出DF=|![]() |=x|
|=x|![]() |=x|
|=x|![]() |=4x,在Rt△DPH中,∠FDG=30°,可得PH′=
|=4x,在Rt△DPH中,∠FDG=30°,可得PH′=![]() DP=2x,由y=S△PDC=
DP=2x,由y=S△PDC=![]() DCPH′求出即可;
DCPH′求出即可;
(2)由(1)知∠FDG=30°,得出∠FDG=∠DCP,以及DP=PC若PH⊥AB则M是DC的中点DM=6,在Rt△DPH中,∠FDG=30°,利用cos∠FDG=![]() 求出AP的长,进而得出x的值;
求出AP的长,进而得出x的值;
(3)分别利用线段AD、FC、BC的长为斜边时求出符合条件的值即可.
试题解析:(1)如图①,过P作PH′⊥AC于H′.
∵DF=DE,
∴∠DFE=∠E
又∵FG=EH,
在△DFG和△DEH中
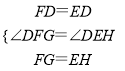 ,
,
∴△DFG≌△DEH(SAS),
∴∠FDG=∠EDH,
∵∠FDE=90°,且∠FDE=∠FDG+∠EDH+∠BAC
∵∠BAC=30°,
∴∠FDG=30°,
∵DF=4,
∴|![]() |=4
|=4
∵![]() =x
=x![]() =x
=x![]() ,
,
∴DP=|![]() |=x|
|=x|![]() |=x|
|=x|![]() |=4x,
|=4x,
在Rt△DPH中,∠FDG=30°,
∴PH′=![]() DP=2x,
DP=2x,
∠B=90°,∠BAC=30°,BC=6,
∴AC=CD=12,
y=S△PDC=![]() DCPH′=
DCPH′=![]() ×122x=12x(x>0);
×122x=12x(x>0);
(2)∵PC∥AB,
∴∠BAC=∠DCP
∵∠BAC=30°,
∴∠DCP=30°,
由(1)知∠FDG=30°,
∴∠FDG=∠DCP,
∴DP=PC
若PH⊥AB,则M是DC的中点DM=6,
在Rt△DPH中,∠FDG=30°,
cos∠FDG=![]() =
=![]() =
=![]() ,
,
∴AP=4![]() ,
,
DP=AP=4x,
∴x=![]() ;
;
(3)如图②,
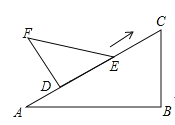
设AD=t,DC=12-t(0<t<12)
FC2=DF2+DC2=42+(12-t)2,
①AD2=FC2+BC2
t2=42+(12-t)2+36
解得:t=![]() (FC至少等于4,故不合题意,舍去)
(FC至少等于4,故不合题意,舍去)
②BC2=FC2+AD2
36=42+(12-t)2+t2,无解,
③FC2=BC2+AD2
∴42+(12-t)2=36+t2
解得t=![]() ,
,
∴当△DEF移动到AD=![]() 时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案