题目内容
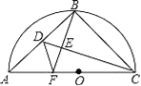
【题目】如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为![]() .
.
(1)求线段AP的长;
(2)若DE是⊙O的切线,求线段OE的长.

【答案】(1)2(2)5
【解析】
(1)根据垂径定理由直径FG⊥AB得到AP=BP=![]() AB=2;
AB=2;
(2)由勾股定理先求得OP,可证△AOP∽△EOC,可得![]() ,即可求得OE.
,即可求得OE.
(1)∵FG为直径,FG⊥AB,AB=4,
∴AP=BP=![]() AB=2;
AB=2;
(2)∵FG⊥AB,AP=2,OA=![]() ,
,
∴在Rt△AOG中,OP=![]() ,
,
在△AOP和△EOC中,
∵∠APO=∠ECO=90°,∠AOP=∠EOC,
∴△AOP∽△EOC,
∴![]() ,
,
即![]() ,
,
∴OE=5.

练习册系列答案
相关题目