题目内容
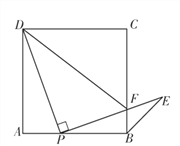
【题目】如图，点P是正方形ABCD边AB上一点（点P不与点A，B重合），连接PD，将线段PD绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F，连接BE，DF.
（1）求∠PBE的度数；
（2）若△PFD∽△BFP，求
的值.
【答案】（1）135°;（2）
.
【解析】整体分析：
(1)过点E作EQ⊥AB交AB的延长线于点Q，证△PAD≌△EQP，得△BQE是等腰直角三角形；(2)由△PFD∽△BFP，得
，由△APD∽△BFP.得
，则AP=BP，即可求解.
解：(1)过点E作EQ⊥AB交AB的延长线于点Q.
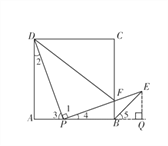
由旋转得PD＝PE，∠DPE=90°.…
∵在正方形ABCD中，∠A=∠ABC=90°，AD=AB，
∴∠EQP=∠A=90°.
∵∠2+∠3=90°，∠3+∠4=90°
∴∠2=∠4.
∴△PAD≌△EQP.
∴EQ=AP，AD=AB=PQ.
∴AP=EQ=BQ.
∴∠5=45°.
∴∠PBE=180°-∠5=135°.
(2)∵△PFD∽△BFP，
∴
.
∵∠A=∠PBC，∠2=∠4，
∴△APD∽△BFP.
∴
.
即
.
∴
.
∴
.
∴
.
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
