题目内容
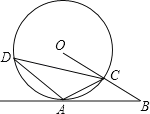
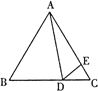
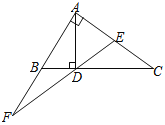
【题目】已知：如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于D，E为直角边AC的中点，过D，E作直线交AB的延长线于F.求证：
＝
.
【答案】见解析
【解析】
首先由直角三角形的性质可得：△CBA∽△ABD，根据相似三角形的对应边成比例，可得：AB：AC=BD：AD，又由直角三角形斜边上的中线是斜边的一半，证得：ED=
AC=EC，可得：∠C=∠EDC，则易得：∠FAD=∠FDB，∠F为公共角，证得：△DBF∽△ADF，则得：BD：AD=DF：AF，则问题得证．
∵∠BAC＝90°，AD⊥BC，∴∠BAC＝∠ADB＝90°，
又∵∠ABC＝∠ABD，
∴△CBA∽△ABD，
∴∠C＝∠FAD，
＝
，∴
＝
，
又∵E为AC的中点，AD⊥BC，
∴ED＝EC＝AC，
∴∠C＝∠EDC，
又∵∠EDC＝∠FDB，
∴∠FAD＝∠FDB，
∵∠F＝∠F，∴△DBF∽△ADF，
∴＝
，
∴＝.
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
