ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓЙ§ЕуЃЈЉ2ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпxЃН1ЃЎгавдЯТНсТлЃК
ЂйabcЃО0ЃЛ
Ђк8a+cЃО0ЃЛ
ЂлШєAЃЈx1ЃЌmЃЉЃЌBЃЈx2ЃЌmЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌЕБxЃНx1+x2ЪБЃЌyЃНcЃЛ
ЂмЕуMЃЌNЪЧХзЮяЯпгыxжсЕФСНИіНЛЕуЃЌШєдкxжсЯТЗНЕФХзЮяЯпЩЯДцдквЛЕуPЃЌЪЙЕУPMЁЭPNЃЌдђaЕФШЁжЕЗЖЮЇЮЊaЁн1ЃЛ
ЂнШєЗНГЬaЃЈx+2ЃЉЃЈ4ЉxЃЉЃНЉ2ЕФСНИљЮЊx1ЃЌx2ЃЌЧвx1ЃМx2ЃЌдђЉ2Ёмx1ЃМx2ЃМ4ЃЎ
ЦфжаНсТле§ШЗЕФгаЃЈЁЁЁЁЃЉ
A. 2ИіB. 3ИіC. 4ИіD. 5Иі
ЁОД№АИЁПA
ЁОНтЮіЁП
ЂйгЩЭМЯѓПЩжЊaЃО0ЃЌcЃМ0ЃЌИљОнЖдГЦжс![]() ЃЌЕУЕНb<0ЃЌМДПЩХаЖЯЃЛ
ЃЌЕУЕНb<0ЃЌМДПЩХаЖЯЃЛ
ЂкгЩЖдГЦжс![]() ЕУЃЌbЃНЉ2aЃЌШЛКѓАбxЃНЉ2ДњШыНтЮіЪНЃЌећРэКѓМДПЩХаЖЯЃЛ
ЕУЃЌbЃНЉ2aЃЌШЛКѓАбxЃНЉ2ДњШыНтЮіЪНЃЌећРэКѓМДПЩХаЖЯЃЛ
ЂлИљОнХзЮяЯпЕФЖдГЦадЃЌЕУx1+x2=2ЃЌШЛКѓАбxЃН2ДњШыНтЮіЪНЃЌМДПЩХаЖЯЃЛ
ЂмгЩЕуMЃЌNЪЧХзЮяЯпгыxжсЕФСНИіНЛЕуЃЌдђХзЮяЯпЕФЖЅЕуЕНxжсЕФОрРыВЛаЁгк3ЃЌдђга![]() ЃЌНсКЯЂкЕФНсТлЃЌМДПЩЧѓЕУaЕФШЁжЕЗЖЮЇЃЛ
ЃЌНсКЯЂкЕФНсТлЃЌМДПЩЧѓЕУaЕФШЁжЕЗЖЮЇЃЛ
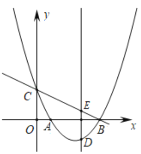
ЂнгЩЭМЯёПЩжЊЃЌгыxжсЕФСНИіНЛЕуЮЊЃЈ-2ЃЌ0ЃЉЃЌЃЈ4ЃЌ0ЃЉЃЌДЫЪБy=0ЃЌдђЕБy=2ЪБЃЌx1ЃМЉ2ЃМ4ЃМx2ЃЌМДПЩЕУЕНД№АИ.
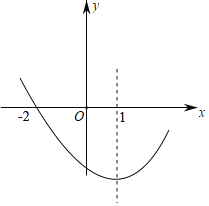
НтЃКЂйгЩЭМЯѓПЩжЊЃКaЃО0ЃЌcЃМ0ЃЌ
![]()
ЁрabcЃО0ЃЌЙЪЂйе§ШЗЃЛ
ЂкЁпХзЮяЯпЕФЖдГЦжсЮЊжБЯпxЃН1ЃЌХзЮяЯпЕФЖдГЦжсЮЊжБЯпxЃН1ЃЌ
![]()
ЁрbЃНЉ2aЃЌ
ЕБxЃНЉ2ЪБЃЌyЃН4aЉ2b+cЃН0ЃЌ
Ёр4a+4a+cЃН0ЃЌ
Ёр8a+cЃН0ЃЌЙЪЂкДэЮѓЃЛ
ЂлЁпAЃЈx1ЃЌmЃЉЃЌBЃЈx2ЃЌmЃЉЪЧХзЮяЯпЩЯЕФСНЕуЃЌ
гЩХзЮяЯпЕФЖдГЦадПЩжЊЃКx1+x2ЃН1ЁС2ЃН2ЃЌ
ЁрЕБxЃН2ЪБЃЌyЃН4a+2b+cЃН4aЉ4a+cЃНcЃЌЙЪЂле§ШЗЃЛ
ЂмгЩЬтвтПЩжЊЃКMЃЌNЕНЖдГЦжсЕФОрРыЮЊ3ЃЌ
ЕБХзЮяЯпЕФЖЅЕуЕНxжсЕФОрРыВЛаЁгк3ЪБЃЌ
дкxжсЯТЗНЕФХзЮяЯпЩЯДцдкЕуPЃЌЪЙЕУPMЁЭPNЃЌ
МД![]() ЃЌ
ЃЌ
Ёп8a+cЃН0ЃЌ
ЁрcЃНЉ8aЃЌ
ЁпbЃНЉ2aЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌЙЪЂмДэЮѓЃЛ
ЃЌЙЪЂмДэЮѓЃЛ
ЂнвзжЊХзЮяЯпгыxжсЕФСэЭтвЛИіНЛЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЌ
ЁрyЃНax2+bx+cЃНaЃЈx+2ЃЉЃЈxЉ4ЃЉ
ШєЗНГЬaЃЈx+2ЃЉЃЈ4ЉxЃЉЃНЉ2ЃЌ
МДЗНГЬaЃЈx+2ЃЉЃЈxЉ4ЃЉЃН2ЕФСНИљЮЊx1ЃЌx2ЃЌ
дђx1ЁЂx2ЮЊХзЮяЯпгыжБЯпyЃН2ЕФСНИіНЛЕуЕФКсзјБъЃЌ
Ёпx1ЃМx2ЃЌ
Ёрx1ЃМЉ2ЃМ4ЃМx2ЃЌЙЪЂнДэЮѓЃЛ
ЙЪбЁЃКAЃЎ

ЁОЬтФПЁПЕцЧђЪЧХХЧђЖгГЃЙцбЕСЗЕФживЊЯюФПжЎвЛЃЎЯТСаЭМБэжаЕФЪ§ОнЪЧМзЁЂввЁЂБћШ§ШЫУПШЫЪЎДЮЕцЧђВтЪдЕФГЩМЈЃЎВтЪдЙцдђЮЊУПДЮСЌајНгЧђ10ИіЃЌУПЕцЧђЕНЮЛ1ИіМЧ1ЗжЃЎ
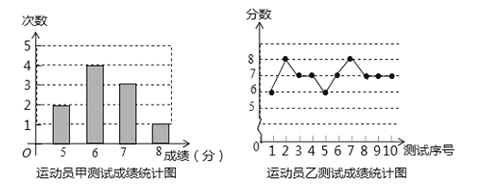
дЫЖЏдББћВтЪдГЩМЈЭГМЦБэ
ВтЪдађКХ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ГЩМЈЃЈЗжЃЉ | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
дЫЖЏдББћВтЪдГЩМЈЕФЦНОљЪ§КЭжкЪ§ЖМЪЧ7ЃЌ
ЃЈ1ЃЉГЩМЈБэжаЕФ![]() __________ЃЌ
__________ЃЌ![]() _________ЃЛ
_________ЃЛ
ЃЈ2ЃЉШєдкЫћУЧШ§ШЫжабЁдёвЛЮЛЕцЧђГЩМЈгХауЧвНЯЮЊЮШЖЈЕФНгЧђФмЪжзїЮЊздгЩШЫЃЌФуШЯЮЊбЁЫИќКЯЪЪЃПЧыгУФуЫљбЇЙ§ЕФЭГМЦСПМгвдЗжЮіЫЕУїЃЈВЮПМЪ§ОнЃКШ§ШЫГЩМЈЕФЗНВюЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЉ
ЃЉ
ЃЈ3ЃЉМзЁЂввЁЂБћШ§ШЫЯрЛЅжЎМфНјааЕцЧђСЗЯАЃЌУПИіШЫЕФЧђЖМЕШПЩФмЕФДЋИјЦфЫћСНШЫЃЌЧђДгввЪжжаДЋГіЃЌЧђДЋвЛДЮМзЕУЕНЧђЕФИХТЪЪЧ____ЃЎ