题目内容
【题目】为了更好营造班级的学习氛围，某中学对九年级六个班有关中考备考宣传墙报进行评比，评分如下：
班级 | 九（1） | 九（2） | 九（3） | 九（4） | 九（5） | 九（6） |
得分 | 95 | 94 | 91 | 90 | 88 | 88 |
（1）求出各班得分的极差、众数、平均数；
（2）本次评比设一、二、三奖，各班均能获奖，具体要求：一等奖的得分＞二等奖的得分＞三等奖的得分，一等奖的名额不能超过2个，三等奖的名额不能少于2个。若从上述方案中任选一种进行评奖，用列举法求出九（3）班获二等奖的概率.
【答案】（1）极差=7， 众数=88 ，平均数=91；(2) P(A)= 
【解析】【试题分析】（1）根据极差的定义。最大值与最小值的差，即95-88=7；众数指出现次数最多的数据，88的出现次数最多，则众数是88；平均数指所有数据之和除以数据的总个数，即
；（2）树状图见解析，从树形图可知，有机会均等的5种情况，故九（3）班获二等奖（记为A）有4种，则P(A)= 
.
【试题解析】
（1）极差=95-88=7
众数=88
平均数=
(2)
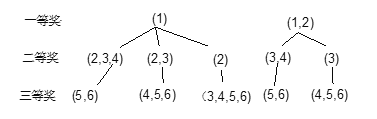
从树形图可知，有机会均等的5种情况，其中九（3）班获二等奖（记为A）有4种
∴ P(A)= 
.
练习册系列答案
相关题目
