题目内容
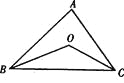
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.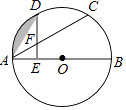
(1)求∠AFE的度数;
(2)求阴影部分的面积(结果保留π和根号).
【答案】
(1)解:连接OD,OC,
∵C、D是半圆O上的三等分点,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴∠AOD=∠DOC=∠COB=60°,
∴∠CAB=30°,
∵DE⊥AB,
∴∠AEF=90°,
∴∠AFE=90°﹣30°=60°;
(2)解:由(1)知,∠AOD=60°,

∵OA=OD,AB=4,
∴△AOD是等边三角形,OA=2,
∵DE⊥AO,
∴DE= ![]() ,
,
∴S阴影=S扇形AOD﹣S△AOD= ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]() π﹣
π﹣ ![]() .
.
【解析】根据题意连接OD,OC,求得∠AOD=∠DOC=∠COB=60°,再根据圆周角定理和直角三角形的性质即可求∠AFE的度数;
(2)由(1)知,∠AOD=60°,求的△AOD是等边三角形,再由DE⊥AO,得到DE的值,再根据扇形和三角形的面积公式即可求出阴影部分的面积.
【考点精析】利用圆周角定理和扇形面积计算公式对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某商场计划用![]() 元从厂家购进
元从厂家购进![]() 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入![]() 台,其中每台的价格、销售获利如下表:
台,其中每台的价格、销售获利如下表:
甲型 | 乙型 | 丙型 | |
价格(元/台) |
|
|
|
销售获利(元/台) |
|
|
|
![]() 购买丙型设备 台(用含
购买丙型设备 台(用含![]() 的代数式表示) ;
的代数式表示) ;
![]() 若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了
若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了![]() 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?
![]() 在第
在第![]() 题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
【题目】小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表.为了节约资金,小明应选择哪一种购买方案?请说明理由.
大笔记本 | 小笔记本 | |
价格(元/本) | 6 | 5 |
页数(页/本) | 100 | 60 |