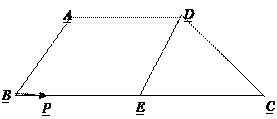题目内容
如图,在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,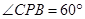 ,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则点B’的坐标是
,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则点B’的坐标是 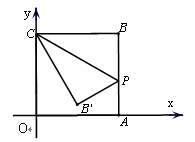
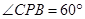 ,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则点B’的坐标是
,沿CP折叠正方形,折叠后,点B落在平面内点B’处,则点B’的坐标是 

过点B′作B′D⊥y轴于D,B′E⊥x轴于E,
∵OABC是正方形,点A的坐标是(4,0),点C的坐标是(0,4),
∴BC=OC=4,
∵∠BPC=60°,
∴由折叠的性质求得B′C=BC=4,∠B′CP=∠BCP=30°
∴∠DCB′=90°﹣∠B′CP﹣∠BCP=30°,
∴B′D=
 B′C=
B′C= CB=2,CD=
CB=2,CD= BC=2
BC=2 ,
,∴OD=OC﹣CD=4﹣2
 ,
,∴B’点的坐标为
 .
.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
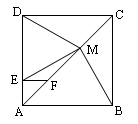
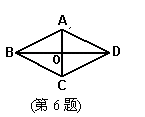
 :MB=MD;
:MB=MD;
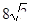 B.
B. 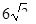 C.
C. 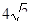 D.
D. 
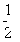 S四边形ABCD
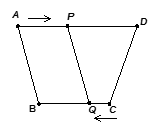
S四边形ABCD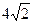 cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。
cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。