题目内容
【题目】“一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.
甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.
设物品的重量为![]() 千克,甲、乙公司快递该物品的费用分别为
千克,甲、乙公司快递该物品的费用分别为![]() .
.
(1)写出![]() 与
与![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
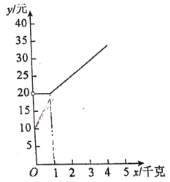
(2)图中给出了![]() 与
与![]() 的函数图象,请在图中画出(1)中的函数图象;
的函数图象,请在图中画出(1)中的函数图象;
(3)小丝需要快递的物品重量为4千克,如果想节省快递费用,结合图象指出,应选择的快递公司是________.
【答案】(1)![]() =7x+10 (x>0);(2)见解析;(3)甲.
=7x+10 (x>0);(2)见解析;(3)甲.
【解析】
(1)根据乙公司的快递费用=7×物品重量+10,即可得出![]() 与x的函数表达式;
与x的函数表达式;
(2)根据一次函数图象上点的坐标特征找出![]() 与x的函数图象经过的两点,描点、连点成线,即可画出(1)中的函数图象;
与x的函数图象经过的两点,描点、连点成线,即可画出(1)中的函数图象;
(3)根据数量关系找出![]() 与x的函数表达式,令
与x的函数表达式,令![]() =
=![]() 求出费用相等时x的值,结合函数图象即可找出结论.
求出费用相等时x的值,结合函数图象即可找出结论.
解:(1)根据题意可知:![]() 与x的函数表达式为:
与x的函数表达式为:![]() =7x+10 (x>0) .
=7x+10 (x>0) .
(2)当x=0时, ![]() =7x+10=10;当x=1时,
=7x+10=10;当x=1时,![]() =7x+10=17.
=7x+10=17.
描点、连点成线,画出函数图象,
如图所示:
(3)根据题意可知:![]() 与x的函数表达式为:
与x的函数表达式为:
![]() .
.
当![]() =
=![]() 时,有7x+10=4x+16,
时,有7x+10=4x+16,
解得:x=2.
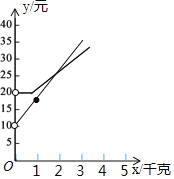
观察函数图象可知:当x>2时,![]() 与x的函数图象在
与x的函数图象在![]() 与x的函数图象的下方,
与x的函数图象的下方,
∴当x=4时,选择甲公司费用较低.
故答案为:甲.

 阅读快车系列答案
阅读快车系列答案【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应数值:
的几组对应数值:
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出![]() 的值为 ;
的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
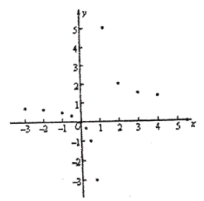
(3)当![]() 时,直接写出x的取值范围为: .
时,直接写出x的取值范围为: .