Question

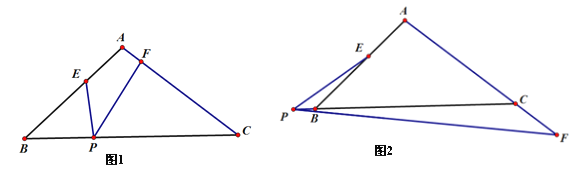
【题目】（1）如图1，△ABC中，∠BAC=100°，AB=AC，P为BC边上任意一点.若点E、F分别在AB、AC上，且∠EPF=40°，求证：△BPE∽△CFP；

（2）如图2，点P在边CB的延长线上，点E在边AB上，点F在边AC的延长线上，仍有∠EPF=40°，探索PB·PC与BE·CF有怎样的关系？并说明理由.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）由已知条件可得∠B=∠C=40°，由∠EPC=∠B+∠BEP，得∠EPF+∠FPC=∠B+∠BEP，而∠EPF=∠B=40°，从而可得∠FPC=∠BEP，从而得到△BPE∽△CFP；

（2）同（1）的道理类似，可得△BPE∽△CFP，从而可得，即PB·PC=BE·CF.

试题解析：（1）∵△ABC中，∠BAC=100°，AB=AC，∴∠B=∠C=40°，∵∠EPC=∠B+∠BEP，∴∠EPF+∠FPC=∠B+∠BEP，又∵∠EPF=∠B=40°，∴∠FPC=∠BEP，∴△BPE∽△CFP；

相等，理由如下：

∵∠EBC=∠EPB+∠BEP，∴∠EPF=∠EPB+∠CPF，又∵∠EPF=∠B=40°，∴∠BEP=∠CPF，∵∠ABC=∠ACB，

∴∠EBP=∠PCF，∴△BPE∽△CFP，∴，∴PB·PC=BE·CF.