题目内容
【题目】某中学七、八年级各选派10名选手参加学校举办的知识竞赛,竞赛计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示.
队别 | 平均分 | 众数 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | a | m | 3.41 | 90% | 20% |
八年级 | 7.1 | p | q | 1.69 | 80% | 10% |
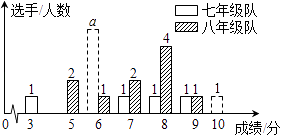
(1)请依据图表中的数据,求出a的值;并直接写出表格中m,p,q的值;
(2)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由、
【答案】
(1)解:根据题意得:3×1+6a+7×1+8×1+9×1+10×1=6.7×10,
解得a=5,七年级成绩为3,6,6,6,6,6,7,8,9,10,中位数为6,即m=6,八年级成绩为5,5,6,7,7,8,8,8,8,9,众数是8,中位数为7.5,即p=8,q=7.5;
(2)解:八年级平均分高于七年级,方差小于七年级,成绩比较稳定,
故八年级队比七年级队成绩好
【解析】(1)根据题中数据求出a、m,p,q的值即可;(2)从方差,平均分角度考虑,给出两条支持八年级队成绩好的理由即可.
【考点精析】解答此题的关键在于理解中位数、众数的相关知识,掌握中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数.

【题目】探索函数y=x+ ![]() 的图象和性质:
的图象和性质:
(1)它的自变量取值范围是;
(2)当x>0时,我们利用列表法画出函数图象
①填写下表,画出函数的图象:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | … |

②观察图象,我们发现函数图象有一个最低点,它的坐标是 ![]() ,这说明当x=
,这说明当x= ![]() ,函数y有最小值是
,函数y有最小值是 ![]() ;并且,在该点的左边,y随x的增大而
;并且,在该点的左边,y随x的增大而 ![]() ,在该点的右边,y随x的增大而
,在该点的右边,y随x的增大而 ![]() .
.
③利用上述结论,解决问题:矩形ABCD的面积等于1,当它的长和宽分别为多少时,它的周长最小?