题目内容
已知: 关于![]() 的方程
的方程![]() ①.(n≠0)
①.(n≠0)
(1)求证: 方程①必有实数根;
(2)若![]() ,
,![]() 为正整数且方程①有两个不相等的整数根时,确定关于
为正整数且方程①有两个不相等的整数根时,确定关于![]() 的二次函数
的二次函数![]() 的解析式;
的解析式;
(3)若把Rt△ABC放在坐标系内,其中∠CAB = 90°,点A、B的坐标分别为(1,0)、(4,0),BC = 5 (点C在第一象限); 将△ABC沿x轴平移,当点C落在抛物线上时,求△ABC平移的距离.
答案:证明:(1)当m=0时,x=1
当m≠0时,∵ ![]()
∴![]()
=![]()
=![]()
∵无论n取何值时,都有![]()
∴![]()
(2)![]()
∴![]()
∴方程①有一个实数根为.
由题意可知:方程①的另一个根为![]()
∵![]() ,
,![]() 为正整数且方程①有两个不相等的整数根
为正整数且方程①有两个不相等的整数根
∴![]()
∴二次函数的解析式:![]()
(3)由题意可知:AB=3,
由勾股定理得:AC=4
∴C点的坐标为(1,4)
当△ABC沿x轴向右平移,此时设C点的坐标为(a,4)
∵ C在抛物线上
∴![]()
![]()
∴![]() ∴
∴![]()
∴△ABC平移的距离:![]() 或
或![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知关于的方程
=-1有正根,则实数a的取值范围是( )
| x+a |
| x-3 |
| A、a<0且a≠-3 |
| B、a>0 |
| C、a<-3 |
| D、a<3且a≠-3 |
 的方程
的方程 .
.
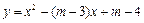 与
与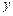 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求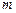 的值.
的值.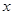 的方程
的方程
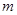 的值,并求出此时方程的根(6分)
的值,并求出此时方程的根(6分)