题目内容
已知关于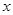 的方程
的方程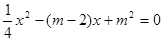
⑴ 若方程有两个相等的实数根,求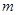 的值,并求出此时方程的根(6分)
的值,并求出此时方程的根(6分)
⑵ 是否存在正数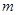 ,使方程的两个实数根的平方和等于224 ?若存在,求出满足条件的
,使方程的两个实数根的平方和等于224 ?若存在,求出满足条件的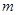 的值; 若不存在,请说明理由。(6分)
的值; 若不存在,请说明理由。(6分)
【答案】
⑴ m=1,x1=x2=-2⑵不存在,理由见解析
【解析】本题考查了根与系数的关系,解一元二次方程-配方法,解一元二次方程-因式分解法,根的判别式. (1)方程有两相等的实数根,利用△=0求出m的值.化简原方程求得方程的根.
(2)利用根与系数的关系x1+x2=-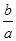 =4m-8,x1x2=
=4m-8,x1x2=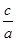 =4m2,x12+x22=(x1+x2)2-2x1x2,代入即可得到关于m的方程,求出m的值,再根据△来判断所求的m的值是否满足原方程.
=4m2,x12+x22=(x1+x2)2-2x1x2,代入即可得到关于m的方程,求出m的值,再根据△来判断所求的m的值是否满足原方程.
解:⑴∵有两个相等的实数根,∴Δ=0,∴[-(m-2)]2—4× ×m2=0,—4m+4=0,
×m2=0,—4m+4=0,
∴m=1.则原方程为: ∴x1=x2=-2。
∴x1=x2=-2。
(2)不存在正数m使方程的两个实数根的平方和等于224.
∵x1+x2=-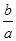 =4m-8,x1x2=
=4m-8,x1x2=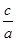 =4m2
=4m2
x12+x22=(x1+x2)2-2x1x2=(4m-8)2-2×4m2=8m2-64m+64=224,
即:8m2-64m-160=0,
解得:m1=10,m2=-2(不合题意,舍去),
又∵m1=10时,△=-4m+4=-36<0,此时方程无实数根,
∴不存在正数m使方程的两个实数根的平方和等于224.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知关于的方程
=-1有正根,则实数a的取值范围是( )
| x+a |
| x-3 |
| A、a<0且a≠-3 |
| B、a>0 |
| C、a<-3 |
| D、a<3且a≠-3 |
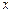 的方程
的方程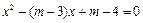 .
.
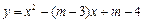 与
与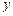 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线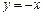 的对称点恰好是点M,求
的对称点恰好是点M,求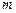 的值.
的值.