题目内容
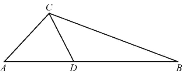
【题目】经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,求∠ACB的度数.
【答案】∠ACB的度数为113°或92°.
【解析】
由△ACD是等腰三角形,∠ADC>∠BCD,推出∠ADC>∠A,即AC≠CD,分两种情形讨论①当AC=AD时,②当DA=DC时,分别求解即可.
:∵△BCD∽△BAC,
∴∠BCD=∠A=46°.
∵△ACD是等腰三角形,∠ADC>∠BCD,
∴∠ADC>∠A,即AC≠CD.
①当AC=AD时,∠ACD=∠ADC=![]() (180°-46°)=67°,
(180°-46°)=67°,
∴∠ACB=67°+46°=113°;②当DA=DC时,∠ACD=∠A=46°,
∴∠ACB=46°+46°=92°.
综上所述,∠ACB的度数为113°或92°.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目