题目内容
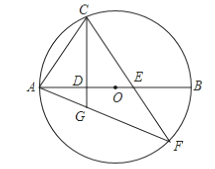
【题目】如图，已知在△ABC外作等腰三角形ABD和等腰三角形ACE，且∠BAD=∠CAE=90°，AM为△ABC中BC边上的中线，连接DE．求证：DE=2AM．
【答案】见解析
【解析】
延长AM到F点，使MF=AF,再连接BF与CF，先证明四边形ABFC是平行四边形，从而利用等量代换得到∠ABF=∠DAE，再根据SAS证明△DAE全等于△ABF，从而进一步证明出结果
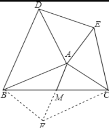
证明：如图，延长AM到F点，使MF=AF,再连接BF与CF
∵AM是BC中线
∴BM=MC
又∵MF=AF
∴四边形ABFC是平行四边形
∴∠ABF＋∠BAC=180°，FB=AC=AE
又∵∠DAE＋∠BAC=180°
∴∠DAE=∠ABF
又∵AD=AB
∴△DAE
△ABF(SAS)
∴DE=AF=2AM
名校课堂系列答案
【题目】如图，在平面直角坐标系中，正方形OABC的顶点A在y轴正半轴上，顶点C在x轴正半轴上，抛物线
（a<0）的顶点为D，且经过点A、B．若△ABD为等腰直角三角形，则a的值为___________．
【题目】下表是某校七～九年级某月课外兴趣小组活动时间统计表，其中各年级同一兴趣小组每次活动时间相同，文艺小组每次活动时间比科技小组每次活动时间多0.5小时.设文艺小组每次活动时间为
小时，请根据表中信息完成下列解答.
课外小组活动 总时间（小时） | 文艺小组 活动次数 | 科技小组 活动次数 | |
七年级 | 12.5 | 4 | 3 |
八年级 | 10.5 | 3 |
|
九年级 | 7 |
|
|
（1）科技小组每次活动时间为______小时（用含的式子表示）；
（2）求八年级科技小组活动次数
的值；
（3）直接写出
______，
______.
【题目】立定跳远是体育中考选考项目之一，体育课上老师记录了某同学的一组立定跳远成绩如表：
成绩（m） | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法，正确的是（ ）
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01