题目内容
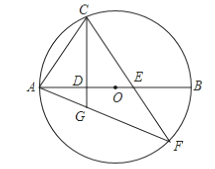
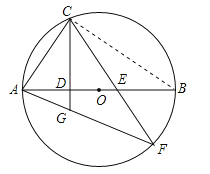
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,连接AC,过点C作直线CD⊥AB于点D,E是AB上一点,直线CE与⊙O交于点F,连结AF,与直线CD交于点G.
求证:(1)∠ACD=∠F; (2)AC2=AG·AF.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)本题可构建相等的中间角通过转换来求解,连接BC,根据圆周角定理得∠ABC=∠F,根据同角的余角相等得∠ACD=∠ABC,由此可得证.
(2)本题实际求的是三角形ACG和AFC相似,已知了一个公共角,而(1)中又证得了∠ACD=∠F,由此可得出两三角形相似,根据相似三角形即可得出所求的比例关系.
试题解析:证明:(1)连接BC,则∠ACB=90°,∠ABC=∠F.∵∠ACD+∠CAD=90°,∠CAD+∠ABC=90°,∴∠ACD=∠ABC,∴∠ACD=∠F.
(2)由(1)得出的∠ACD=∠F.又∵∠CAG=∠FAC,∴△ACG∽△AFC,∴ ![]() ,∴AC2=AGAF.
,∴AC2=AGAF.

练习册系列答案
相关题目
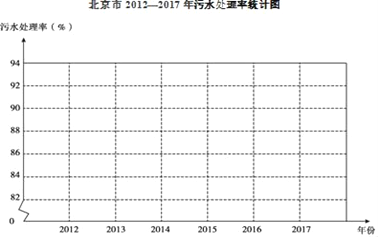
【题目】北京市积极开展城市环境建设,其中污水治理是重点工作之一,以下是北京市2012﹣2017年污水处理率统计表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
污水处理率(%) | 83.0 | 84.6 | 86.1 | 87.9 | 90.0 | 92.0 |
(1)用折线图将2012﹣2017年北京市污水处理率表示出来,并在图中标明相应的数据;
(2)根据统计图表中提供的信息,预估2018年北京市污水处理率约为_____%,说明你的预估理由:_____.