题目内容
如图,在直角坐标系中,抛物线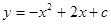 与
与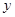 轴交于点D(0,3).
轴交于点D(0,3).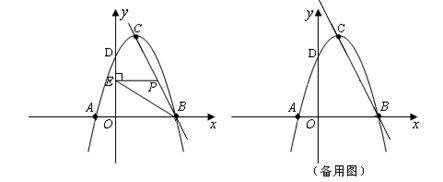
【小题1】直接写出
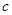 的值;
的值;【小题2】若抛物线与
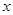 轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;【小题3】已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥
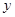 轴,垂足为E,连结BE.设点P的坐标为(
轴,垂足为E,连结BE.设点P的坐标为(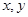 ),△PBE的面积为
),△PBE的面积为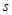 ,求
,求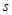 与
与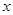 的函数关系式,写出自变量
的函数关系式,写出自变量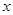 的取值范围,并求出
的取值范围,并求出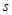 的最大值;
的最大值;②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为
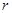 的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求
的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求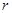 的值,并直接写出点P的坐标;如果不存在,请说明理由.
的值,并直接写出点P的坐标;如果不存在,请说明理由.
p;【答案】
【小题1】 .……………………………(2分)
.……………………………(2分)
【小题2】由(1)知抛物线为:

∴顶点C坐标为(1,4) ……………………………(3分)
令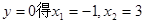 ∴ B(3,0)……………………(4分)
∴ B(3,0)……………………(4分)
设直线BC解析式为: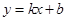 (
(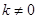 ),把B、C两点坐标代入,
),把B、C两点坐标代入,
得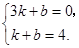 解得
解得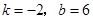 .
.
∴直线BC解析式为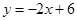 .……………………(5分)
.……………………(5分)
【小题3】①∵点P(x,y)在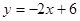 的图象上,
的图象上,
∴PE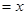 ,OE
,OE ……………………(6分)
……………………(6分)
∴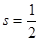 PE·OE
PE·OE
∴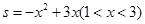 ………………(7分)
………………(7分)
 .
.
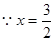 符合
符合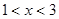 ,
,
∴当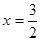 时,s取得最大值,最大值为
时,s取得最大值,最大值为 .……(8分)
.……(8分)
②答:存在.
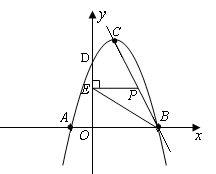
如图,设抛物线的对称轴交x轴于点F,则CF=4,BF=2.

过P作PQ⊥CF于Q,则Rt△CPQ∽Rt△CBF
∴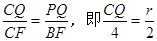 ∴CQ=2r……………(9分)
∴CQ=2r……………(9分)
当⊙P与⊙C外切时,CP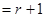 .
.
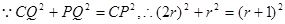
解得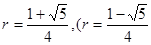 舍去).……………(10分)
舍去).……………(10分)
此时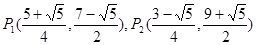 .……………………(11分)
.……………………(11分)
当⊙P与⊙C内切时,CP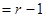 .
.
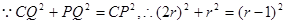 .
.
解得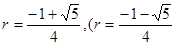 舍去).……………………(12分)
舍去).……………………(12分)
此时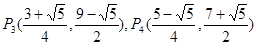 .
.
∴当 时,⊙P与⊙C相切.
时,⊙P与⊙C相切.
点P的坐标为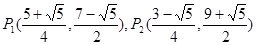 ,
,
 .……………………(13分)解析:
.……………………(13分)解析:
略
【小题1】
 .……………………………(2分)
.……………………………(2分)【小题2】由(1)知抛物线为:

∴顶点C坐标为(1,4) ……………………………(3分)
令
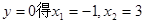 ∴ B(3,0)……………………(4分)
∴ B(3,0)……………………(4分)设直线BC解析式为:
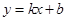 (
(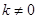 ),把B、C两点坐标代入,
),把B、C两点坐标代入,得
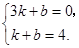 解得
解得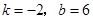 .
.∴直线BC解析式为
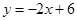 .……………………(5分)
.……………………(5分)【小题3】①∵点P(x,y)在
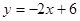 的图象上,
的图象上,
∴PE
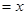 ,OE
,OE ……………………(6分)
……………………(6分)∴
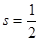 PE·OE
PE·OE
∴
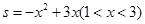 ………………(7分)
………………(7分) .
.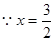 符合
符合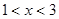 ,
,∴当
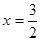 时,s取得最大值,最大值为
时,s取得最大值,最大值为 .……(8分)
.……(8分)②答:存在.
如图,设抛物线的对称轴交x轴于点F,则CF=4,BF=2.

过P作PQ⊥CF于Q,则Rt△CPQ∽Rt△CBF
∴
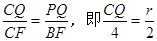 ∴CQ=2r……………(9分)
∴CQ=2r……………(9分)当⊙P与⊙C外切时,CP
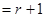 .
.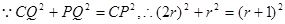
解得
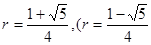 舍去).……………(10分)
舍去).……………(10分)此时
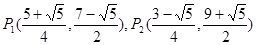 .……………………(11分)
.……………………(11分)当⊙P与⊙C内切时,CP
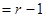 .
.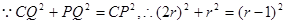 .
.解得
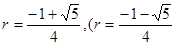 舍去).……………………(12分)
舍去).……………………(12分)此时
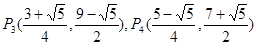 .
.∴当
 时,⊙P与⊙C相切.
时,⊙P与⊙C相切.点P的坐标为
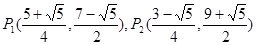 ,
, .……………………(13分)解析:
.……………………(13分)解析:略

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: